Пример №6.

Дано: Е =32 В, R_ВН=1 Ом, R₁=10 Ом, R₂=15 Ом, R₃=25 Ом, R₄=25 Ом,
R₅=12,5 Ом. (Рис. 6)

Определить: Эквивалентное сопротивление всей цепи R_ЭКВ и токи в ветвях.

Рис. 6а. Рис. 6б.

Рис. 6в. Рис. 6г. Рис. 6д.

Решение.

Выберем направление неизвестных токов I, I₁, I₂, I_3, I₄, I₅произвольным образом (как показано на рис. 6а). Обозначим места соединения элементов электрической цепи точками A, B, C, D. Как видно из рис. 6а. в электрической схеме нет ни последовательного, ни параллельного, ни смешанного соединения резисторов. Следовательно, эту задачу решим преобразовав резисторы с сопротивлениями R₁, R₂, R₃, соединенные треугольником АВС в эквивалентную звезду с сопротивлениями R_А, R_В, R_С. Для этого мысленно опускаем лучи из узлов А, В, С в одну общую точку О (узел 0). Можно доказать, что сопротивления резисторов, находящихся на этих лучах, вычисляются по формулам:

После проведенных преобразований резисторы R₁, R₂, R₃ из исходной схемы исключаются, в результате получаем следующую эквивалентную схему. (Рис. 6б.) В этой схеме токи I₄, I₅, I остаются теми же самыми (по величине и по направлению), что и на рис. 6а, поскольку данная часть схемы не была затронута выполненным преобразованием.

Анализ электрической схемы рис. 6б показывает, что резисторы с сопротивлениями R_А и R₄, а также резисторы с сопротивлениями R_С и R₅ включены последовательно. Заменим их на эквивалентные им резисторы с сопротивлениями R_А4 и соответственно R_С5 :

Получаем следующую эквивалентную схему 6в. В данной схеме сопротивления R_А4 и R_С5 включены параллельно. Заменим их на эквивалентный им резистор с сопротивлением R_OD, рассчитанным по формуле:

После проведенного преобразования схема 6в трансформируется в схему 6г, в которой резисторы с сопротивлениями R_В, R_OD, R_ВН включены между собой последовательно. Заменим их на общий эквивалентный им резистор с сопротивлением R_ЭКВ, найденным по формуле:

Получаем окончательную эквивалентную схему замещения (рис. 6д) исходной расчетной схемы (рис. 6а).

Зная общее эквивалентное сопротивление цепи можно найти ток I, протекающий через источник ЭДС Е:

Чтобы найти токи I₄ и I₅, протекающие через соответствующие резисторы с сопротивлениями R_А4 и R_С5 необходимо определить падение напряжения U_OD (рис 6г):

Следовательно,

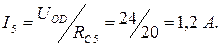(См. рис. 6в)

Чтобы вычислить ток I₃ необходимо знать падение напряжения U_AC, которое определим по второму закону Кирхгофа, выбрав положительный обход контура ADCА по часовой стрелке, как показано на рис. 6а:

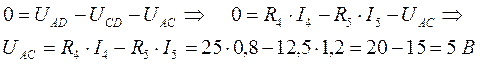
Следовательно,

Токи I₁ и I₂ определим по первому закону Кирхгофа соответственно для узлов А и С:

узел А: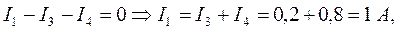

узел С:

Правильность расчетов любой электрической цепи проверяется по законам Кирхгофа, но наиболее достоверная проверка получается лишь по балансу электрических мощностей:

Где - алгебраическая сумма мощностей, выделяемых источниками ЭДС Е, слагаемое этой суммы берется со знаком «+», если направления ЭДС источника и тока, протекающего через него совпадают между собой, в противном случае берется знак «-».

Где - арифметическая сумма мощностей, потребляемых приемниками (в нашем случае резисторами).

ПРИМЕЧАНИЕ. Баланс мощностей составляется для исходной схемы с учетом истинных направлений токов.

Проверим правильность проведенных расчетов по балансу мощностей:

64 Вт=64 Вт.

Согласно балансу электрических мощностей, расчеты проведены корректно.

Ту же самую задачу можно решить, воспользовавшись эквивалентным преобразованием резисторов с сопротивлениями R₁, R₃, R₄, соединенных звездой в треугольник с эквивалентными резисторами с сопротивлениями
R₁₃, R₃₄, R₁₄. Для этого объединим выходы В, С, D резисторов R₁, R₃, R₄ между собой через соответствующие резисторы R₁₃, R₃₄, R₁₄, которые рассчитаем по формулам:

После такого преобразования резисторы с сопротивлениями R₁, R₃, R₄ исключаются из исходной схемы. В результате получаем преобразованную схему (рис. 7б).

Рис. 7в. Рис. 7г. Рис. 7д.

Как видно из рис. 7б резисторы с сопротивлениями R₂ и R₁₃, а также R₅ и R₃₄ включены между собой параллельно.

Следовательно,

Преобразуем электрическую схему 7б в электрическую схему 7в. Поскольку резисторы с сопротивлениями R_ВС и R_CD включены последовательно, то (Рис. 7г)

Общее эквивалентное сопротивление всей цепи с учетом внутреннего сопротивления источника ЭДС определяется:

Зная общее эквивалентное сопротивление всей цепи, вычислим ток, протекающий через источник ЭДС:

Используя второй закон Кирхгофа для замкнутого контура BDB определим падение напряжения между точками В и D (см. рис 7г):

Рассчитаем промежуточный ток I_BCD (см. рис. 7г):

Найдем падения напряжений U_BC и U_CD из рис. 7в:

Теперь определим неизвестные токи I₂ и I₅ из рис. 7б:

Вычислим неизвестные токи I₁ и I₄ по первому закону Кирхгофа, составленных для соответственно узлов В и D (см. рис. 7а):

узел В:

узел D: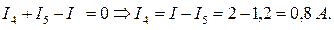

Для определения оставшегося неизвестного тока I₃ воспользуемся вторым законом Кирхгофа для замкнутого контура ВАСВ:

Как следует из проведенных вычислений любой способ эквивалентного преобразования треугольника в звезду или наоборот дает один и тот же искомый результат, естественно, при четком соблюдении правил и порядка расчетов.