Решение. Направим произвольным образом реальные неизвестные токи I1, I2, I3

Направим произвольным образом реальные неизвестные токи I₁, I₂, I₃. Поскольку в расчетной схеме два независимых контура (1,11,10,2,3,4,5,6,1) и (1,7,8,9,2,10,11,1), то контурных токов должно быть тоже два, соответственно I₁₁, I₂₂. Выберем произвольным образом направление контурных токов, например, по часовой стрелке (см. рис. 14).

Составим два линейных уравнения относительно неизвестных контурных токов I₁₁, I₂₂, используя второй закон Кирхгофа.

Вначале определяем все падения напряжения в первом контуре от протекающего в нем контурного тока I₁₁ со знаком «+»:

а затем все падения напряжения от контурного тока I₂₂, протекающего через участок 2,10,11,1 этого же контура, но со знаком «-»: .

Таким же образом определяются падения напряжения для второго контура.

Следовательно:

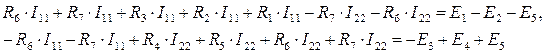
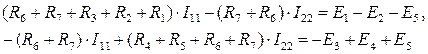
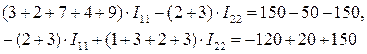
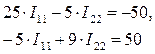
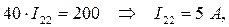
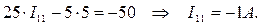
Согласно данному методу величина и направление выбранных контурных токов I₁₁ и I₂₂ соответствует искомым физическим токам соответственно I₁ и I₂ (см. рис. 14).

ПРИМЕЧАНИЕ. Данное утверждение дается без доказательств.

Следовательно, I₁= I₁₁=-1 А, а I₂=I₂₂=5 А.

Знак «-» тока I₁ означает, что истинное направление тока должно быть противоположно рассчитанному. На схеме истинное направление тока I₁ показано пунктиром.

Ток I₃ определим по первому закону Кирхгофа для узла 1:

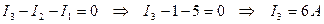
Правильность проведенных расчетов проверим по балансу мощностей:

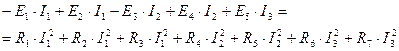
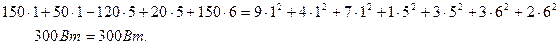
Построим потенциальную диаграмму для замкнутого контура 3456178923 .

Пусть потенциал φ₃=0, тогда φ₄= φ₃+R₂ ·I₁ = 0+4·1=4 В,

φ₅= φ₄+Е₁ = 4+150=154 В,

φ₆= φ₅+R₁ ·I₁ = 154+9·1=163 В,

φ₁= φ₆ – Е₂ = 163 – 50=113 В,

φ₇= φ₁ – R₄ ·I₂ = 113 – 1·5=108 В,

φ₈= φ₇ – Е₃ = 108 – 120= –12 В,

φ₉= φ₈ – R₅ ·I₂ = –12 – 3·5= –27 В,

φ₂= φ₉+Е₄ = –27+20= –7 В,

φ₃= φ₂+R₃ ·I₁ = –7+7·1=0 В.

Графически потенциальная диаграмма выглядит следующим образом (рис. 15):

Рис. 15

3. МЕТОД ДВУХ УЗЛОВ

Данный метод базируется на обобщенном законе Ома и первом законе Кирхгофа и применяется при расчетах электрических цепей с двумя узлами (т.е. электрическая цепь с параллельно соединенными ветвями). При решении задач данным методом в начале определяется падение напряжения между этими двумя узлами по формуле:

,

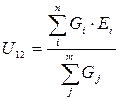где G_i , G_j – электрические проводимости соответствующих ветвей,

G_j×E_i – произведение электрической проводимости ветви на ЭДС Е той же самой ветви, которое берется со знаком «+», если ЭДС Е направлено к узлу 1, в противном случае берется знак «-».

После определения падения напряжения между двумя узлами рассчитывается неизвестные токи по обобщенному закону Ома (см. пример 10).

Применение метода двух узлов рассмотрим на конкретном числовом примере. В качестве примера возьмем ту же самую задачу, что и в предыдущем случае (см. пример №12).