Ортодромическая поправка и способы ее расчета.

Форма и модели Земли. Общий земной эллипсоид. Эллипсоид Красовского. Главные радиусы кривизны. Длина 1 минуты дуги меридиана. Морские единицы длины и скорости. Система географических координат.

Форма и модели Земли:Плотность масс Земли в её толще распределена чрезвычайно неравномерно, поэтому уровенная поверхность образует сложное в математическом отношении трёхмерное тело. Эта фигура имеющая неправильную геометрическую форму называется геоидом, что в переводе с греческого означает «землеподобный».

Общий земной эллипсоид: Для решения задач морской навигации используют аппроксимацию (приближение) геоида телом неправильной математической формы. Это тело – эллипсоид вращения, полученный в результате вращения эллипса вокруг малой оси. Другими словами, геоид заменяют его моделью. Сочетание геоида, а также эллипсоида по экватору и меридиану 80Е…100W.

Эллипсоид Красовского: Для геодезических и картографических расчётов в определённых районах Земли необходимо иметь земной эллипсоид, поверхность которого максимально совпадает с поверхностью этого района. Очевидно, что такой эллипсоид должен иметь вполне определённые ориентацию и размеры. Это референц-эллипсоид. В конкретном государстве к нему и относят измерения на земной поверхности.

В России в качестве референц-эллипсоида принят референц-эллипсоид Ф. Н. Красовского. Этот референц-эллипсоид вычислен группой учёных под руководством профессора Ф. Н. Красовского. Модель имеет следующие параметры:

- Большая полуось a = 6378245 м;

- Малая полуось b = 6356863 м;

- Полярное сжатие a = (a –b) / a = 1/298.3;

- Эксцентриситет e =Ö(a²-b²) / a = 0.0818

Отклонения данного эллипсоида от геоида на территории нашей страны не превышает 150 м.

Для референц-эллипсоида Красовского радиус модели Земли как шара равен:

R = 6371110 м.

В качестве модели геоида для спутниковых навигационных систем в настоящее время используется модель WGS-84 (World Geodetic System – 1984).

Главные радиусы кривизны:
Главными нормальными сечениями на поверхности эллипсоида являются меридианное сечение и сечение по первому вертикалу.

Радиус кривизны Μ меридианного сечения Pn e Ps q имеет минимальное значение:

Видно, что радиус кривизны меридианного сечения Μ зависит от широты места и имеет максимальное значение на полюсах (φ = = 90°), а минимальное значение на экваторе (φ = 0°).
С помощью радиуса кривизны меридианного сечения Μ рассчитывается длина одной минуты дуги меридиана земного эллипсоида:

Видно, что длина одной минуты дуги меридиана является величиной переменной и зависит от широты места. Наименьшая длина 1' дуги меридиана у экватора — 1842,98 м, наибольшая у полюсов — 1861,57 м.
Сечение по первому вертикалу EKW (рис. 1.8) перпендикулярно меридианному сечению в данной точке.

Радиус кривизны сечения по первому вертикалу N имеет максимальное значение и его величина определяется выражением

С помощью радиуса кривизны сечения по первому вертикалу определяется радиус параллели в любой заданной широте φ. Так, радиус параллели точки K определяется по формуле

Длина одной минуты параллели

Общая кривизна поверхности земного эллипсоида в данной точке характеризуется средним радиусом

Морские единицы длины и скорости:Метрическая система неудобна для измерений расстояний на море, так как в процессе судовождения приходится решать задачи, связанные с измерением углов и угловых расстояний.

Стандартная морская миля соответствует длине минуты меридиана референц-эллипсоида Красовского на широте 44⁰ 18’. Она отличается от значений на полюсах и экваторе всего на 0,5%.

Одна десятая часть морской мили называется кабельтов (кб) 1кб = 0,1 мили = 185,2 м

За единицу скорости в морской навигации принят узел (уз) – 1уз = 1 миля/час.

Переход от скорости в узлах к скорости в кабельтовых в минуту производится по формуле:

V_кб/мин = V_уз/6

При расчетах, связанных со скоростью ветра, и в других случаях используется единица метр в секунду (м/с) – 1м/с = 2уз.

Система географических координат:В зависимости от избранной модели Земли и решаемых задач для определения положения точек на земной поверхности используют различные системы координат: географические, сферические, астрономические, полярные, прямоугольные. Для определения положения точек на поверхности эллипсоида (сфероида) в судовождении используется система географических (сфероидических) координат.

В географической системе координат координатными осями являются экватор (рис. 1.5) и один из меридианов, называемый нулевым (начальным).
За нулевой меридиан при измерении географических долгот принят меридиан Гринвича. Начало координат — в точке пересечения экватора с Гринвичским меридианом. Координатными линиями являются параллели и меридианы, а координатами — географическая широта и географическая долгота.

Географической широтой точки А называется угол между плоскостью экватора и нормалью к поверхности земного эллипсоида в этой точке. Географическая широта обозначается греческой буквой φ и измеряется дугой меридиана от экватора до параллели данной точки.

Географической долготой точки А называется двугранный угол между плоскостью Гринвичского меридиана и плоскостью меридиана данной точки. Географическая долгота обозначается греческой буквой λ и измеряется меньшей дугой экватора от Гринвичского меридиана до меридиана данной точки.

2. Картографическая проекция Меркатора, её уравнения и свойства. Изменение масштаба в меркаторской проекции. Меридиональные части. Главная параллель карты.

Меркаторская проекция – прямая равноугольная цилиндрическая.

Примем Землю за шар, уменьшим его до необходимых размеров. Будем рассматривать эту модель как условный глобус, масштаб которого равен главному масштабу будущей карты.

Поместим глобус в цилиндр, так чтобы по экватору он касался поверхности цилиндра, при этом ось цилиндра совмещается с осью глобуса.

Масштаб карты изменяется пропорционально широте (sec φ).

Степень растяжения параллели пропорциональна sec широты: R=r*cos φ

Где R – радиус экватора;

r - радиус произвольной параллели.

Меридиональные части – расстояние в минутах дуги экватора до выбранной параллели от экватора.

Меркаторская миля – отношение одной минуты длины меридиана к знаменателю масштаба карты.

Главная параллель – параллель вдоль которой сохраняется главный масштаб карты.

3. Картографическая проекция Гaycca, её уравнения и свойства. Картографическая сетка, схождение меридианов. Система плоских прямоугольных координат.

Проекция Гаусса – равноугольная поперечная цилиндрическая проекция. Проекция осуществляется по частям, зонами шириной 6 градусов долготы. Началом координат каждой зоны является точка пересечения осевого меридиана с экватором.

Свойства: Равноугольная

Масштаб сохраняется на всей поверхности карты

Ортодромичность

Уравнение равноугольной поперечной цилиндрической проекции Гаусса, выражающее связь географических координат точки на поверхности Земли с плоскими координатами на карте, имеют вид:

Анализ полученных уравнений позволяет определить основные свойства проекции:

- Координаты линии x и y – прямые, при этом линии x параллельны осеннему меридиану, а линии у параллельны экватору, т.е. линии х и у являются взаимно перпендикулярными прямыми;

- масштаб карты по оси Х (по осевому меридиану) не изменяется;

- масштаб карты по оси У теоретически возрастает с удалением от осевого меридиана пропорционально sec Y/R.

4. Локсодромия, ее уравнение и свойства:

Кривую на поверхности Земли, пересекающую все меридианы под одним и тем же углом, называют локсодромией, что с греческого переводится как «косой бег».

Расстояние между двумя точками на сфере по локсодромии не является кратчайшим и её применение в мореплавании объясняется исключительным удобством использования компасов.

Основные свойства локсодромии:

1. Если К = 0 или 180⁰, то очевидно, что локсодромия совпадает с меридианом, то есть с большим кругом.

2. Если К = 90⁰ или 270⁰, то локсодромия совпадает с параллелью или экватором, то есть образует малый или большой круг на поверхности сферы.

3. При любых других курсах локсодромия спиралеобразно стремится к полюсу, никогда его не достигая.

Уравнение локсодромии для эллипсоида:

Более краткая запись выглядит так:

,

где V_1,2 – изометрическая широта.

,

5. Ортодромия, ее уравнение и свойства:

На шаре линией кратчайшего расстояния является дуга большого круга (ДБК), которую называют ортодромией. В переводе с греческого языка ортос - прямой, дромос - проход, бег.

При необходимости решения задач на эллипсоиде пользуются поправками за сфероидичность Земли, выбираемыми из специальных таблиц, помещенных в сборнике "Мореходные таблицы".
Через две произвольные точки шара В1 и В2 (рис. 1.9) можно провести только одну ортодромию, так как плоскость ДБК проведена через три точки: В1, В2 и центр Земли.
Треугольник МВ1b1 прямоугольный, так как меридиан пересекается с экватором в точке M под углом 90°. Поскольку стороны этого треугольника являются дугами окружностей больших кругов, то решают его, используя формулы сферической тригонометрии.
Применяя к треугольнику МВ1b1 формулу тангенса катета прямоугольного сферического треугольника, можно записать

Это выражение справедливо для любой точки ортодромии, поэтому полученное выражение является ее уравнением:

где λ0 и А0 — параметры ДБК (λ0 — долгота пересечения ДБК с экватором, Ao — направление ДБК в этой точке). Для определения Ao и λ0 используют формулы:

ДБК достигает максимальной широты в точке V, которая называется "вертекс". Вертексов два: один в северном полушарии (виден на рисунке), другой — в южном.
Координаты вертекса:

Проанализируем полученные выражения с целью определения свойств ортодромии.

Свойства ортодромии.
1. Из выражения (1.18) и рис. 1.9 видно, что меридиан вертекса является плоскостью симметрии ортодромии. То есть ортодромия пересекает каждый меридиан два раза в долготах:

λi и λi'= 2λν — λi

2. Из выражения (1.17):
если Аo = 90° (270°), то ортодромия совпадает с меридианом, если Ao = 0° (180°), то ортодромия совпадает с экватором.
3. Из выражения (1.14) видно, что если неоднократно изменять долготу λ на 360° (предположим, что совершается кругосветное путешествие по ортодромии), то правая часть уравнения не изменяется. Не изменится и левая часть — широта постоянна. Значит ортодромия пересекает каждый меридиан каждый раз в одной и той же точке. Ортодромия — замкнутая кривая.

4. Судоводителей особо интересует направление ортодромии, то есть угол А, под которым ортодромия пересекает меридианы (курс ортодромии). Применяя теорему четырех рядом лежащих элементов сферической тригонометрии к треугольнику Β1ΡΝΒ2, после преобразований получим:

Видно, что А = f(φi,λi), т. е. курс ДБК зависит от координат точек В1 и В2. Следовательно, ортодромия пересекает все меридианы под различными углами:

Разность углов, под которыми ортодромия пересекает меридианы двух точек, называется схождением (сближением) меридианов и обозначается буквой γ (гамма) греческого алфавита:

Формула для расчета γ может быть выведена из сферического треугольника Β1ΡΝΒ2 . Для этого следует использовать формулы сферической тригонометрии, называемые аналогиями Непера

Применяя их к сферическому треугольнику Β1ΡΝΒ2, получим:

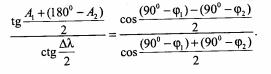
После преобразований

Обозначим: — средняя широта.

Считая, что при плавании на расстояния до 500 миль получим:
Вместе с тем на малых расстояниях угол γ тоже мал:

тогда γ = Δλsin φcp.
Следует заметить, что угол γ имеет знак, который зависит как от знака Δλ, так и от знака φcp.
При всех своих преимуществах ортодромия неудобна для плавания, так как для удержания на ней судна пришлось бы непрерывно изменять его курс.

Ортодромическая поправка и способы ее расчета.

В практике судовождения широко используются и ортодромия и локсодромия. Возникает необходимость переходить от ортодромических направлений к локсодромическим и наоборот.
На рис. 1.12 через две произвольные точки В1 и В2 проведены отрезки локсодромии и ортодромии. Разность направлений ортодромии и локсодромии в этих точках обозначена буквой ψ (пси) греческого алфавита.
Угол между ортодромией и локсодромией, проходящими через две заданные точки, называется ортодромической поправкой.
На расстояниях до 500 миль можно считать ортодромию и локсодромию расположенными симметрично, и тогда
ψ1 = ψ2 = Ψ·
Из рис. 1.12 для точки B1 : ψ1 = K-Al;
для точки В2: ψ2 = А2 — К.
Сложим: 2ψ = А2 — А1
но А2 — А1 = γ , поэтому ψ = 0,5γ

или ψ = 0,5Δλsinφcp.
Если расстояние между точками В1 и В2 больше 500 миль, то

ψ2 не равно ψ2. В этом случае необходим непосредственный расчет ортодромической поправки как разности направлений локсодромии и ортодромии по формуле
ψ = К-А.
Для облегчения расчета ортодромической поправки на малых расстояниях в Мореходных таблицах (МТ-2000) помещена табл. 2.12.
Следует иметь в виду, что угол ψ имеет знак, который зависит как от знака Δλ , так и от знака sinφcp. Правило знаков приведено в МТ-2000 в объяснении к таблице.