
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вопрос 4. Виды признаков. Связи между ними. Оценка тесноты связи
Признак – это качественная особенность единицы совокупности.
Все признаки можно классифицировать на:
1) факторные, т.е. обуславливающие изменения другого признака. Обозначаются: х
2) результативные, т.е. изменяющиеся под влиянием других признаков. Обозначаются: y
А связимежду признаками можно разделить по типам:
- функциональная(жестко детерминированная). Каждому значению факторного признака х соответствует одно или несколько жестко определенных значений y;
- статистическая (стохастическая). Среднее значение результативного признака зависит от изменения факторного, т.е. при конкретном значении х, y может принимать различные значения из определенного интервала с разными вероятностями.
Частный случай статистической связи – корреляционная связь. Она заключается в том, что различным значениям одной переменной могут соответствовать различные значения другой переменной.
Виды связей:
а) по направлению:
- прямая (с увеличением х, у увеличивается и наоборот),
- обратная (с увеличением х, у уменьшается и наоборот)
б) по аналитическому выражению:
- линейная (у=ах+в),
- нелинейные (любая кривая)
в) по степени тесноты связей:
- сильная,
- умеренная,
- слабая,
- отсутствует.
Регрессия– определение формы связи между признаками
Корреляция – определение тесноты силы связи.
Оценка существенности/тесноты связей:
- коэффициент эластичности: 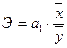
Данный коэффициент показывает на сколько % изменится значение результативного признака при изменении факторного на 1%.
- коэффициент Фихнера: основан на количестве совпадений и несовпадений знаков отношений значений признаков от их средних значений 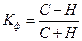 , где С – число совпадений, Н – число несовпадений.
, где С – число совпадений, Н – число несовпадений.
- линейный коэффициент корреляции: применяется только для линейных связей 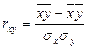
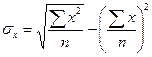
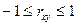
Если  >0, то связь прямая, если
>0, то связь прямая, если  <0, то связь обратная, если
<0, то связь обратная, если  =0, то связи нет
=0, то связи нет

- корреляционное отношение: применяется для любых связей 
- коэффициент детерминации: показывает сколько % вариации результативного признака объясняется вариацией факторного 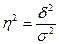 , для линейных связей
, для линейных связей 
Оценка связи качественных явлений
- для таблиц 2х2
коэффициент ассоциации 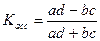
коэффициент контингенции 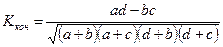
Если Касс>0,5 и Ккон>0,3, то связь значимая
| довольны з/п | не довольны | ||
| частные предприятия | a | b | a+b |
| государственные | c | d | c+d |
| a+c | b+d | a+b+c+d |
- для таблиц больших, чем 2х2
nxy – элемент таблицы, где х – номер строки, у – номер столбца
- коэффициенты взаимной сопряженности Пирсона и Чупрова
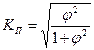 ,
, 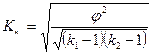 , где k1 и k2 – количество строк и столбцов
, где k1 и k2 – количество строк и столбцов
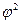 - показатель взаимной сопряженности,
- показатель взаимной сопряженности, 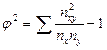
Коэффициенты Пирсона и Чупрова можно также рассчитать через критерий Пирсона 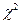
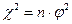 , тогда
, тогда 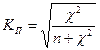 ,
, 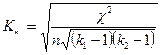
Ранговые коэффициенты
Ранг – это порядковый номер значения признака в порядке возрастания или убывания. Ранжирование это упорядочивание значений в порядке предпочтения. Некоторые значения признака иногда имеют одинаковую количественную оценку, в этом случае ранг всех этих значений будет равен среднему арифметическому от соответствующих номеров мест. Такие ранги называются связанные.
- коэффициент Спирмена:
- если нет связанных рангов 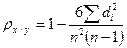 , где n – число наблюдений,
, где n – число наблюдений, 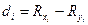
- если есть связанные ранги  , где
, где 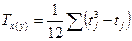 , tj – количество одинаковых рангов
, tj – количество одинаковых рангов
- коэффициент Кендалла:
- если нет связанных рангов 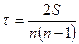 , n – число пар рангов, S – сумма разностей между числом последовательностей и числом инверсий
, n – число пар рангов, S – сумма разностей между числом последовательностей и числом инверсий
- если есть связанные ранги 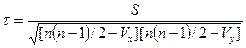 , где
, где 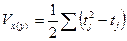 , tj – количество одинаковых рангов
, tj – количество одинаковых рангов
Связь считается значимой, если значения коэффициентов Спирмена и Кендалла больше 0,5.
- коэффициент конкордации:
Характеризует тесноту связи между произвольным числом ранжированных признаков.
 , где S – отклонение суммы квадратов рангов от средней квадратов рангов, n – число наблюдений, m – количество факторов
, где S – отклонение суммы квадратов рангов от средней квадратов рангов, n – число наблюдений, m – количество факторов
Если есть связанные ранги, то 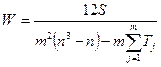 , где
, где 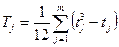
Дата добавления: 2015-04-18; просмотров: 300; Мы поможем в написании вашей работы!; Нарушение авторских прав |