Вопрос 1. Показатели вариации. Правило сложения дисперсий

Вариация – это изменение ("колеблемость") величины, либо значения признака при переходе от одного объекта (или группы объектов) к другому; точнее говоря – от одной единицы совокупности к другой. Обычно под вариацией мы понимаем обусловленное перекрещивающимся влиянием различных факторов на данное явление изменение величин только в пределах однородной совокупности.

Конкретные условия, в которых находится каждый из изучаемых объектов, а также особенности их собственного развития (социальные, экономические и пр.) выражаются соответствующими числовыми уровнями статистических показателей. Таким образом, вариация, т.е. несовпадение уровней одного и того же показателя у разных объектов, имеет объективный характер и помогает познать сущность изучаемого явления.

Все показатели делятся на абсолютные и относительные.

Абсолютные показатели вариации:

- R – размах вариации,

, где X_max,min – максимальное и минимальное значение признака

- среднее линейное отклонение – это среднее отклонение от среднего уровня

(если данные не сгруппированы) – простая формула

При повторяемости отдельных значений Х используют формулу средней арифметической взвешенной:

(взвешенное среднее линейное отклонение)

(Следует отметить, что алгебраическая сумма отклонений от среднего уровня равна нулю).

Показатель среднего линейного отклонения нашел широкое применение на практике. С его помощью анализируются, например, состав работающих, ритмичность производства, равномерность поставок материалов. Но, также следует заметить, что этот показатель усложняет расчеты вероятностного типа, затрудняет применение методов математической статистики. Поэтому в статистических научных исследованиях для измерения вариации чаще всего применяют показатель дисперсии.

- дисперсия (средний квадрат отклонений от средней)

Дисперсия признака ( ) определяется на основе квадратической степенной средней:

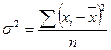(невзвешенная формула) или (взвешенная формула)

- Показатель s, равный , называется средним квадратическим отклонением.