
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теорема Винера-Хинчина.
(Иванов, 3.6)
Найдём связь между распределением спектральной плотности мощности и видом корреляционной функции. Как известно корреляционная функция сигнала связана преобразованием Фурье с его энергетическим спектром. Применим это свойство к отрезку реализации процесса длительностью  :
:
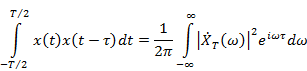
Где  — спектральная плотность. Разделим обе части равенства на
— спектральная плотность. Разделим обе части равенства на  и устремим
и устремим  к бесконечности:
к бесконечности:
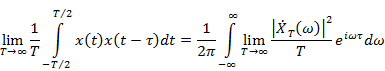
Если считать процесс эргодичным, то слева стоит корреляционная функция, а справа под интегралом стоит выражение для спектральной плотности мощности 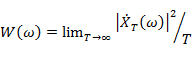 . С учётом этого получаем:
. С учётом этого получаем:
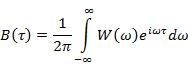
Таким образом, корреляционная функция случайного процесса и его плотность мощности связаны друг с другом преобразованием Фурье. Это соотношение носит название теоремы Винера-Хинчина. Так как функции 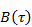 и
и  являются чётными и вещественными, то можно отказаться от комплексной формы записи:
являются чётными и вещественными, то можно отказаться от комплексной формы записи:
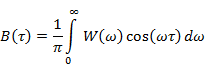

Дата добавления: 2015-04-18; просмотров: 520; Мы поможем в написании вашей работы!; Нарушение авторских прав |