Понятие о ширине спектра и интервале корреляции.

( http://siblec.ru/index.php?dn=html&way=bW9kL2h0bWwvY29udGVudC84c2VtLzA2Ni9zNS01Lmh0bQ )

При спектральных преобразованиях случайных процессов важное значение приобретает ширина спектра процесса. Эффективная ширина энергетического спектра определяется следующим образом:

Где — спектральная плотность. Этому определению можно дать графическую интерпретацию. На рис. 5.7 изображена кривая одностороннего энергетического спектра (на нём вместо X стоит G). Построим прямоугольник с площадью, равной площади по кривой , одна сторона которого составляет величину . Тогда вторая сторона прямоугольника будет характеризовать эффективную ширину энергетического спектра .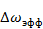

Представим последнее выражение в виде:

Левая сторона этого равенства представляет собой среднюю мощность случайного процесса с равномерным энергетическим спектром в пределах полосы частот 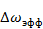, а правая – среднюю мощность рассматриваемого случайного процесса.

Автокорреляционная функция случайного процесса характеризует степень статистической связи между значениями процесса, разделенными интервалом времени . При этом, для эргодических процессов, которые изучаются в радиотехнике, автокорреляционная функция стремится к нулю при неограниченном возрастании . Очевидно, при определенном значении , значения случайного процесса и можно считать статистически несвязанными (некоррелированными). Такое значение называется интервалом корреляции.

Интервал корреляции определяется в соответствии с выражением

Где 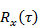— нормированная автокорреляционная функция. На рис. 5.8 приведена графическая интерпретация понятия интервала корреляции. Интервал корреляции представляет собой сторону прямоугольника, по площади равному площади под кривой при .

Установим связь между эффективной шириной спектра и интервалом корреляции в предположении, что , а функция корреляции представляет собой неотрицательную монотонно убывающую функцию, что позволяет в последнем выражении полагать :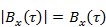

Таким образом, произведение эффективной ширины спектра и интервала корреляции представляет собой постоянную величину. Из этого вытекает, что чем шире энергетический спектр, тем меньше интервал корреляции между его значениями и наоборот.