Теорема Котельника для временной функции.

Любой сигнал, передаваемый по реальной системе связи и управления, имеет ограниченный частотный спектр. В этом случае справедлива теорема Котельникова, утверждающая, что сигнал с ограниченным спектром полностью определяется своими значениями(выборками), взятыми через интервалы времени 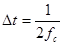, где 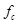-частота среза (верхняя граничная частота сигнала). По этим значениям непрерывный сигнал может быть полностью восстановлен на выходе системы.

Действительно, пусть функции , описывающей передаваемый сигнал, соответствует спектральная функция отличная от нуля в полосе частот от 0 до 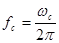, тогда на основании обратного преобразования Фурье представим в виде (1)

В момент времени , где - любое целое число, значение функции определится выражением , (2)

С другой стороны известно, что функция , заданная на интервале частот между и , может быть представлена рядом Фурье (путем ее периодического продолжения с периодом на весь интервал частот от до + ) в виде , (3)

где согласно преобразованию Фурье (4)

Из сравнения (2) и (4) следует (5)

Таким образом, коэффициенты Фурье в разложении (2) пропорциональны значениям функции в дискретные моменты времени . Разложение (3) при известных значениях коэффициентов полностью определяет функцию на интервале . Но так как функция является спектральной характеристикой функции , то и эта последняя также полностью определена. Следовательно, знания значений функции в моменты времени достаточно для полного определения функции , что и доказывает теорему.

Воспользовавшись (1), (2) и (5), получим

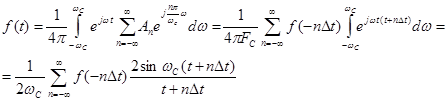
Так как суммирование производится по положительным и отрицательным целым числам , знаки перед можно изменить на обратные и тогда получим (6)

Представленное разложение (6) называется рядом Котельникова. Слагаемые этого ряда представляют собой произведения выборок из сигнала на “включающие” функции типа . Как известно, такую форму отклика имеет идеальный фильтр низкой частоты (ФНЧ) на -функцию.

Метод формирования непрерывного сигнала из слагаемых ряда Котельникова поясняет рис.1., где сверху изображена некоторая функция с ограниченным спектром. В точках взяты отсчеты - они представлены соответствующими ординатами. На последующих строках рисунка изображены отдельные слагаемые ряда (5). Они представляются колебаниями типа , но сдвинутыми друг относительно друга на . Если теперь сложить все эти ординаты, то получится снова исходная функция Заметим, что в точке ая составляющая равна , а все остальные составляющие равны нулю.

Разложение (5) указывает технический способ передачи функции с ограниченным спектром и восстановления ее на приемном конце. Способ этот состоит из следующих операций:

1. Берутся отсчеты функции в моменты .

2. Полученные числа передаются любым способом по системе связи.

3. На приемном конце вырабатываются короткие импульсы соответствующей высоты.

4. Эти импульсы подаются на вход идеального фильтра низкой частоты (ФНЧ) с верхней границей полосы пропускания . На выходе фильтра получается исходная функция .