I. Решение телеграфных уравнений для линии без потерь

=0; =0)

Это идеализация задачи позволяет раскрыть сущность физических процессов характерных для цепей с распределёнными параметрами.

Уравнения (160) в этом случае приобретают вид:

(161)

Продифференцируем по xи t систему (161а). Тогда получим

(161а)

Отсюда следует, что функция uудовлетворяет волновому уравнению:

Аналогично для тока где ;

Общее решение (162) может быть представлено в виде:

(164)

причём функции и определяются конкретным условием задачи.

Выясним смысл ( ) и ( ) из (164) .Рассмотрим вначале функцию . Её значения в один и тот же момент времени зависит от x, но можно подобрать да момента времени и для координат и соответственно так , что будет выполняться равенство

Это справедливо , если ; пусть 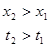, тогда

и, наконец, отсюда

(165)

отсюда следует, что постоянное значение функции движется по оси xсо скоростью, определяемой из (165) и зависящей от погонных параметров линии. Это свойство функции даёт основание называть её волновой функцией или волной (идущей в право)

Очевидно, что описывает волну идущую влево (отражённую) . Для тока в линии можно записать аналогичное решение

(166)

Чтобы установить связь между напряжением и током в линии, подставим эти решения в систему (161) , например в первое уравнение:

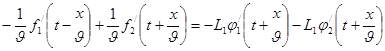
Это равенство выполняется при любых t и x,если

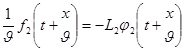
Отсюда следует, что

Эти соотношения можно привести к виду:

, где ; (167)

Величина называется волновым сопротивлением линии.

Оно в данном случае чисто активно.

Рассмотрим прямую волну. Если напряжение в x=0 равно t , то напряжение и ток в xравны:

где U-амплитуда напряжения переменной волны

-амплитуда тока переменной волны

- волновое число.

Отсюда видно, что текущие фазы (ωt-βx) напряжения и тока при t=Const зависят от x и характеризуется величиной β для данного x, поэтому β и называется коэффициентом фазы или волновым числом. На длине волны фаза, как известно, меняется на , поэтому ; и , т.е.

зависит от L₁C₁. Отсюда видно, что волновой характер процессов в линии будет проявляться слабо, если ее длина много меньше длины волны т.е. если . Следовательно линию можно считать длинной в том случае, если ее длина по крайней мере соизмерима с длиной волны. Что касается расстояния между проводами, образующими линию, то оно выбирается много меньше длины волны.

В теории линий величину электрической длиной.