Преобразование спектров в нелинейных цепях.

(Баскаков, 11.2)

В нелинейных системах связь между входным сигналом и выходной реакцией устанавливается нелинейной функциональной зависимостью

Будем рассматривать внешние характеристики нелинейных двухполюсников, когда входным сигналом служит напряжение 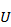, а выходным — ток . Зависимость принято называть вольт-амперной характеристикой (ВАХ) нелинейного элемента.

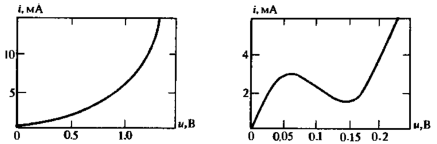
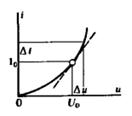Понятие сопротивление для линейного двухполюсника можно определить по-разному. Приложив к двухполюснику постоянное напряжение , получим цепи ток . Отношение называют сопротивление элемента постоянному току. Отношение приращения напряжения к приращению тока в выбранной рабочей точке называют дифференциальным сопротивлением нелинейного двухполюсника: или дифференциальной крутизной ВАХ: .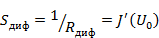

Рассмотрим последовательность соединения источника сигнала , источника постоянного напряжения смещения 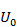и нелинейного элемента с ВАХ . На рисунке ниже показано, как нелинейный элемент искажает сигнал.

Пусть 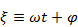. Тогда функция оказывает периодичной относительно аргумента с периодом , поэтому её можно разложить в ряд Фурье:

Где

Так как чётная, то ряд Фурье можно упростить:

Где

Таким образом, из простого гармонического сигнала с частотой получился сигнал с гармониками .