II Решение телеграфных уравнений для линий с потерями.

Пусть ЭДС генератора синусоидальна, т.е. и , где

U(x) и I(x)- комплексные амплитуды напряжения и тока соответственно.

Подставляя это в уравнение (160) получим:

(168)

Продифференцируем (168) по x:

Решение (169): (171), где (172) называется постоянной распространения.

Для тока из (168) запишем или

(173), где 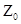равно (174) и

представляет собой волновое сопротивление линии с потерями. Из формул (172) и (174) следует, что в линии с потерями и 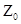является комплексными:

(175)

Выясним физический смысл , , . Для этого рассмотрим прямую волну.

(176)

Переходя к мгновенным значениям, и полагая, что начальная фаза в точке x=0 равна нулю, получим:

(177)

Отсюда следует, что распространение волны вдоль линии с потерями сопровождается экспоненциальным затуханием амплитуд. Скорость затухания зависит от , называемое коэффициентом затухания. Коэффициент - волновое число. Угол характеризует сдвиг фаз между напряжением и током прямой волны в любой точке x.