Детерминированные и стохастические системы. Их анализ.

В зависимости от того, учитываются ли в математической модели системы случайные факторы или нет, модель может быть стохастической или детерминированной. В стохастических системах, в отличие от детерминированных, учитываются случайные факторы, для которых может быть либо известен закон распределения, либо нет. Учет вероятностных факторов в системе существенно осложняет задачу, так как выходные характеристики системы в этом случае тоже становятся случайными величинами и для определения их вероятностных характеристик необходимо использовать специальный метод расчета - метод статистических испытаний.

Рассмотрим метод Доступова: метод эквивалентных возмущений.

Пусть система описывается системой ДУ:

.

Здесь v - вектор случайных величин, воздействующих на систему, с нулевым математическим ожиданием и с диагональной корреляционной матрицей.

Интегрируя каким-либо способом это ДУ, мы получим зависимость . Из решения видно, что решение - функция случайных аргументов v. Поэтому характеризовать эту функцию при разных значениях t можно и нужно математическим ожиданием и дисперсией. Найдём выражения для вычисления математического ожидания функции. Для этого разложим эту функцию в ряд Тейлора с учётом квадратичных членов разложения.

Осуществим операцию вычисления математического ожидания:

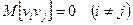
Для вычисления дисперсии воспользуемся свойством

Неудобством данного алгоритма является необходимость вычисления и 1-ых и 2-ых производных. Избежать этого можно следующим образом: задаём L наборов случайных величин

Проинтегрируем исходное уравнение L раз при этих наборах случайных величин. Получим L значений функций . Значения теперь можно записать в следующем виде:

Умножим на неопределённый пока коэффициент .

и сложим левые и правые части.

Теперь наша задача заключается в том, чтобы подобрать так, чтобы это сложное выражение было равно математической ожиданию от x.

Выполнение этого условия можно достигнуть, представив возмущения в следующем виде:

Необходимо найти и , используя полученные условия для и значений случайных величин. Получим: