Оценка внутренней стоимости акций

Среди финансовых активов выделяются так называемым капитальные финансовые активы — акции и облигации. Именно с помощью этих инструментов формируется капитал фирмы, они являются одновременно и объектами, и способами реализации двух типовых финансовых процессов — мобилизации (с помощью эмиссии акций и облигаций привлекается капитал на долгосрочной основе) и инвестирования (в акции и облигации вкладываются свободные денежные средства как в долгосрочных, так и в краткосрочных целях).

Применительно к акциям первые разработки в области теории оценивания на фондовом рынке в рамках фундаменталистского подхода связывают с именем выпускника Гарвардского университета Дж. Уильямса ( John В. Williams ), который в своей докторской диссертации, написанной в 1937 г., предложил в качестве одного из инструментов для работы на рынке ценных бумаг модель оценки акций, основанную на дисконтировании дивидендов, выплачиваемых в денежной форме:

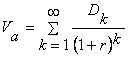
(2.2.4)

где V а — теоретическая (внутренняя) стоимость обыкновенной акции;

Dk — выплаченный дивиденд в k-м периоде;

г — коэффициент дисконтирования.

Сложность применения этой формулы связана с невозможностью точно предсказать величину будущих дивидендов. Исключение составляют привилегированные акции. Привилегированные акции генерируют доход неопределенно долго, равными выплатами через равные промежутки времени, т.е. поток платежей представляет собой бессрочный аннуитет. Поэтому их текущая теоретическая стоимость, равная приведенной доходности, определяется по формуле (2.1.18):

где V па – внутренняя стоимость привилегированной акции;

D – величина дивиденда, в рублях;

r – рыночная норма прибыли по акциям данного класса риска.

Эмиссия бессрочных привилегированных акций, предусматривающих выплату дивиденда по постоянной ставке, является довольно рисковым мероприятием, поскольку невозможно спрогнозировать процентные ставки на длительную перспективу. Поэтому иногда привилегированные акции эмитируются на условиях, позволяющих эмитенту выкупить их в определенный момент времени по соответствующей цене, называемой ценой выкупа (Рв). В этом случае текущая теоретическая стоимость таких акций определяется по формуле:

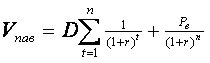
(2.2.6)

где V пав – внутренняя стоимость выкупаемой привилегированной акции;

D – величина дивиденда, в рублях;

r – рыночная норма прибыли по акциям данного класса риска;

n – число периодов до выкупа акций эмитентом;

Рв – выкупная цена акции.

Что касается обыкновенных акций, то известны различные методы их оценки; наиболее распространенным из них является метод, основанный на оценке их будущих поступлений, т.е. на применении формулы (2.2.4). В зависимости от предполагаемой динамики дивидендов конкретное представление формулы меняется. Базовыми являются три варианта динамики прогнозных значений дивидендов:

• дивиденды не меняются (ситуация аналогична ситуации с привилегированными акциями, т.е. применяется формула (2.1.18);
• дивиденды возрастают с постоянным темпом прироста;
• дивиденды возрастают с изменяющимся темпом прироста.

Рассмотрим оценку акций с равномерно возрастающими дивидендами

Предполагается, что базовая величина дивиденда (т.е. последнего выплаченного дивиденда) равна D; ежегодно она увеличивается с темпом прироста g . Например, по окончании первого года будет выплачен дивиденд в размере D × (1 + g ) и т.д. Тогда формула (2.2.1) примет вид:

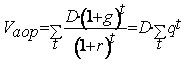
(2.2.7)

Используя формулу суммы членов геометрической прогрессии, можно показать, что:

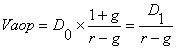
(2.2.8)

где V_аор – внутренняя стоимость обыкновенной акции с равномерно возрастающими дивидендами;

D ₀ – дивиденд в базисном периоде;

g – темп прироста дивидендов (в долях от единицы);

r – ставка дисконтирования;

D ₁ – дивиденд в первом прогнозном периоде.

Данная формула имеет смысл при r > g и называется моделью Гордона.

Из формулы (2.2.8) видно, что текущая цена обыкновенной акции очень чувствительна к параметру g. Даже незначительное его изменение может существенно повлиять на цену. Поэтому в расчетах иногда пытаются разбить интервал прогнозирования на подынтервалы, каждый из которых характеризуется собственным темпом прироста g. Так, если выделить два подынтервала с темпами прироста g и р соответственно, то формула (2.2.7) принимает вид:

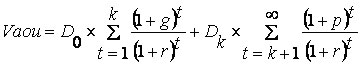
(2.2.9)

где V аои – внутренняя стоимость обыкновенной акции с периодически изменяющимся темпом роста дивидендов;

D 0 — дивиденд, выплаченный в базисный момент времени;

Dk — прогноз дивиденда в k -м периоде;

k – номер периода, в котором изменяется темп роста дивидендов;

g — прогноз темпа прироста дивиденда в первые k лет;

р — прогноз темпа прироста дивидендов в последующие годы.

При выделении нескольких подпериодов модель становится более громоздкой в представлении, однако вычислительные процедуры достаточно просты.

Типичной является ситуация, когда в течение непродолжительного подпериода темп прироста может быть сравнительно высоким, причем не обязательно одинаковым, а затем он снижается и становится постоянным.

В этом случае внутренняя стоимость акции складывается из двух слагаемых – первое (для первого подпериода) на основе формулы (2.2.1); второе – для второго подпериода на основе формулы (2.2.5). Итоговая формула для оценки внутренней стоимости акции имеет вид:

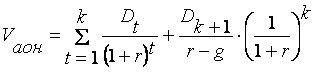
(2.2.10)

где V аон – внутренняя стоимость обыкновенной акции с частично неравномерным темпом роста дивидендов;

D_t— дивиденд, ожидаемый в t -ом году;

D_k+1— прогноз дивиденда в ( k +1)-м году;

k – номер года, в котором устанавливается постоянный темп прироста дивидендов;

g — прогноз темпа прироста дивиденда k -м и последующих годах.