Доходность облигаций. Оценка стоимости облигации выполняется по формуле (2.2.13)

Оценка стоимости облигации выполняется по формуле (2.2.13). Эта же формула может использоваться для оценки доходности облигации. В этом случае V опд – текущая рыночная цена облигации – известна, а неизвестна величина r. Решение уравнения относительно г определяет доходность данной облигации. Этот показатель иногда называется доходностью к погашению и обозначается YTM ( Yield to Maturity ). В условиях эффективного рынка все облигации одного класса теоретически должны иметь примерно одинаковую доходность.

Для приблизительной оценки доходности купонной облигации без права досрочного погашения рассчитывается отношение среднегодового дохода (годовой процент плюс часть разницы между номинальной стоимостью и ценой покупки облигации) к средней величине инвестиции:

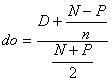
(2.5.3)

где do — доходность облигации;

N — номинал облигации;

Р — текущая цена (на момент оценки);

D — купонный доход;

n — число лет, оставшихся до погашения облигации.

Достоинством показателя do , как и любого другого показателя эффективности, является возможность использования его в сравнительном анализе при выборе вариантов инвестирования в те или иные облигации. Формула (2.5.3) обеспечивает достаточную точность расчетов.

В некоторых отечественных пособиях по финансовому анализу для оценки эффективности инвестирования в облигации рекомендуют ориентироваться на показатель текущей, или дивидендной, доходности, под которым понимается отношение дохода, получаемого ежегодно по купонной ставке, к фактическим затратам на приобретение облигации:

(2.5.4)

где dot – текущая доходность облигации;

N – номинальная стоимость облигации;

P – текущая рыночная стоимость облигации;

k – купонная ставка.

Из формулы (2.5.4) видно, что показатель текущей доходности не может использоваться в качестве обобщенной характеристики и критерия при анализе целесообразности инвестирования в данные облигации. Он дает искаженную оценку доходности облигации, поскольку не учтитывает доход ее держателя, полученный от приобретения облигации с дисконтом.

Еще одной характеристикой доходности облигации является показатель купонной доходности, рассчитываемый по следующей формуле:

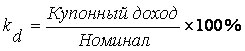
(2.5.5)

Чаще всего этот показатель не рассчитывается, а задается в виде купонной ставки. Значимость этого показателя для оценки доходности облигации невысока, а именно: эта ставка дает оценку доходности облигации лишь в момент ее эмиссии; в дальнейшем она используется в основном для расчета купонного дохода.

Облигации с правом досрочного погашения имеют, кроме рассмотренных, еще одну характеристику — доходность досрочного погашения ( Yield to Call , YTC). Этот показатель дает оценку доходности на момент отзыва облигации с рынка, или ее досрочного погашения. По аналогии с общей доходностью показатель YTC находится из формулы (2.2.13), в которой номинал N заменен выкупной ценой Р.

Конвертируемая облигация предусматривает при выполнении некоторых условий возможность ее обмена на n -е число обыкновенных акций эмитента. Обмен может осуществляться, например, на основании коэффициента конверсии r с. В этом случае облигация имеет так называемую конверсионную стоимость (Рс), которая связана с рыночной ценой базисного актива (обыкновенной акции) Р s следующим соотношением:

(2.5.6)

Оценка ожидаемой доходности конвертируемой облигации находится из формулы (2.2.13), в которой номинал N заменен ожидаемой конверсионной стоимостью. Основным моментом в процессе анализа является установление прогнозной оценки стоимости базисного актива на тот или иной момент времени.