Зертханалық жұмыс.Стокс әдісі бойынша сұйықтың тұтқырлық коэффициентін анықтау(гицерин мен мотор майын салыстыру).

Тұтқыр сұйықта қозғалатын кез-келген денеге кедергі күші əсер етеді. Жалпы жағдайда осы кедергі күшінің шамасы көптеген факторларға

тəуелді: сұйықтың ішкі үйкелісіне, дененің сыртқы пішініне, қалай айналып өтуіне жəне т.б. Стокс шарикті шексіз сұйықтың ламинарлы айналып өтуі жөніндегі есептің дəл шешімін алған. Бұл жағдайда F кедергі күші мына формуламен анықталады:

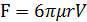(1.1)

мұндағы µ- сұйықтың ішкі үйкеліс коэффициенті(сұйықтың динамикалық тұтқырлығы), V- шариктің жылдамдығы, r– шариктің радиусы. Стокс формуласын гидродинамикалық қорытып шығаруы өте қиын. Сондықтан

өлшемділік ториясының көмегімен есепті талдаумен ғана шектелейік.

Тəжірибеден төмен қарай құлдилап келе жатқан шариктің ішкі үйкеліс коэффициенті µ, радиусы жəне жылдамдығы неғұрлым көп болса, соғұрлым оның кедергі күші де көп болатынын көреміз. Сайып келгенде, былай жазуға болады:

(1.2)

бірақ, басқа жағынан Ньютон формуласы бойынша

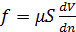(1.3)

(1.2) жəне(1.3) қатынастарын салыстыра отырып, шамасы

мөлшерлілігіне ие болу керек екендігін көреміз.

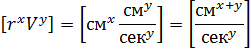
ал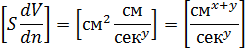

онда

Осыдан

⇒

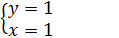
Демек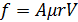

А көбейткішін бұл əдіспен анықтау мүмкін емес, егер тұтқыр сұйық гидродинамикасының есебін шешетін болсақ, онда ол π 6 -ге тең болады екен. Сұйықтың бойымен төмен қарай құлдилаған шариктің қозғалысын қарастырған жағдайда қозғалыс теңдеуі мына түрде болады

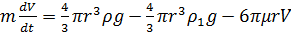(1.4)

мұндағы ρ − шарик жасалған материалдың тығыздығы; − сұйықтың тығыздығы; g − ауырлық күшінің үдеуі. (1.4) теңдеуінің оң жағына кіретін күштердің үшеуі де вертикаль бойымен бағытталады: ауырлық күші– төмен қарай, көтеру күші мен кедергі күші– жоғары қарай. Шариктің қозғалыс жылдамдығы өскен сайын кедергі күшінің шамасы да

артады, ал үдеуі азаяды, тіптен ең аяғында шарик үдеуі нөлге тең болатындай жылдамдыққа жетеді, сонда(1.4) теңдеуінің түрі былай болады.

(1.5)

Бұл жағдайда шарик тұрақты жылдамдықпен қозғалады.Шариктің мұндай қозғалысын орнықталған қозғалыс деп атайды.

(1.5) теңдеуін ішкі үйкеліс коэффициентіне қатысты шешіп, мына шаманы аламыз:

(1.6)

Теңдіктің оң жағында тұрған шамаларды білген жағдайда сұйықтың ішкі үйкеліс коэффициентін анықтауға болады. Шариктің шексіз ортада төмен қарай құлдилауын болдыру практикалық жағдайда шын мəнінде мүмкін емес, себебі сұйық əрқашанда қабырғасы бар ыдыстың ішінде болады. Егер шарик радиусы R-ге тең цилиндрлік ыдыстың өзегін бойлай құласа, онда ыдыстың қабырғасының бар екендігін ескерген кездегі тұтқырлық коэффициенті келесі өрнекпен өрнектеледі/2/|.

(1.7)

Ыдыстың түбі жəне сұйықтың беті сияқты шекаралардың бар екендігі бұл формулада ескерілмейді.