Поверхности

На эту элементарную площадку нормально к цилиндрической поверхности будет действовать сила избыточного гидростатиче­ского давления , которую можно разложить на гори­зонтальную и вертикальную составляющие, т. е. на силы dp_x и dp_z,.

Предположим, что сила dp наклонена к горизонту под углом a. Тогда выражения для составляющих сил могут быть записаны так: dp_x = dp cos a и dp_z = dp sin a.

Подставив значение dp в выражение dp_x, получим:

dp_x=ghdw cos a.

Согласно рис. 2.18, dwcosa=dw_z, т. е. проекция элементар­ной полоски dw на вертикальную плоскость. Следовательно, можно записать, что dp_x=ghdw_z. Тогда горизонтальная состав­ляющая полной силы избыточного гидростатического давления на рассматриваемую цилиндрическую поверхность будет опреде­ляться как

.

Здесь интеграл — статический момент всей площади верти­кальной проекции цилиндрической поверхности относительно свободной поверхности жидкости. Этот статический момент ра­вен произведению площади вертикальной проекции цилиндриче­ской поверхности на глубину погружения центра ее тяжести h_c, т. е.

.

Таким образом, горизонтальная составляющая силы избы­точного гидростатического давления, действующего на цилинд­рическую поверхность, равна силе гидростатического давления, под действием которого находится вертикальная стена, по пло­щади равная площади вертикальной проекции рассматриваемой цилиндрической поверхности:

.

Величина этой горизонтальной составляющей может быть также выражена площадью эпюры гидростатического давле­ния СЕЕ'.

Для определения вертикальной составляющей элементарной силы избыточного гидростатического давления можно написать:

.

Величина является площадью проекции , элемен­тарной площадки на горизонтальную плоскость. Совершенно очевидно, что выражение 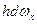представляет собой объем dV призмы, отмеченной на рис. 2.18 штриховкой. Произведение же является массой жидкости в этом бесконечно малом объ­еме, т. е.

dM=gdV.

Тогда вертикальная составляющая полной силы избыточного гидростатического давления равна

.

Центр давления для цилиндрических поверхностей находится графоаналитическим путем.

Вектор полной силы давления Р должен проходить через точ­ку пересечения ее горизонтальной и вертикальной составляющих

P_X и Р_Z под углом b, определяемым из выражения . В данном случае центр давления будет расположен в точке пересечения вектора полной силы давления с криволинейной поверхностью АВ (точка D).