
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Графическое представление и практическое применение уравнения Бернулли
Диаграмма уравнения Бернулли для потока реальной жидкости показана на рис. 3.4. От центров тяжести сечений / и // отложены отрезки, соответственно равные пьезометрическим высотам  и
и  , затем от точек В и В1 отложены вверх отрезки,соответствующие высотам скоростного напора в этих сечениях
, затем от точек В и В1 отложены вверх отрезки,соответствующие высотам скоростного напора в этих сечениях
Линия О—О - след плоскости сравнения; линия ВВ' называется пьезометрической линией; линия СС' — напорной линией; линия DD' — линией первоначального напора. Очевидно, отрезок D'C' соответствует потере напора hw по длине потока на участке между сечениями / — //.
На основании уравнения Бернулли сконструирован ряд приборов, такие, как , водоструйный насос, эжектор и др.
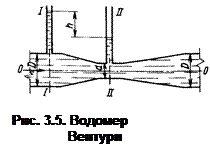 |
Рассмотрим применение уравнения Бернулли на примере водомерного устройства в трубах — водомера Вентури (рис. 3.5), представляющего собой вставку в основную трубу диаметром D трубы меньшего диаметра d, которая соединена с основной трубой коническими переходами. В основной трубе (сечение 1—1) и в суженном сечении (сечение //—//) присоединены пьезометры, по показаниям которых и определим расход жидкости Q в трубе.
Выведем общую формулу водомера для определения расхода жидкости.
Предварительно приняв для заданных условий z1=z2=0, a1=1 и a2=1 и hw=0 (ввиду малости расстояния между сечениями), можем записать уравнения Бернулли в виде:
 .
.
Отсюда следует, что с увеличением скорости движения пьезометрическое давление уменьшается и наоборот. Это положение используется в водомере Вентури, где по разности показаний пьезометров h, зная диаметры D и d, можно определить мгновенный поток.

где  и
и  - площади соответствующих сечений
- площади соответствующих сечений
 |
В водоструйном насосе (рис. 3.6) вода из бака 1 поступает в трубу, имеющую сужение. В узком сечении трубы скорость струи возрастает. При этом в соответствии с уравнением Бернулли давление здесь падает ниже атмосферного, благодаря чему происходит подсасывание жидкости по трубке, опущенной в бак 2. При больших скоростях движения жидкость будет подсасываться из бака 2 непрерывно.
Скорость течения движущейся жидкости можно определить трубкой Пито. Этот прибор (рис. 3.7) представляет собой стеклянную трубку, открытую с двух концов. При этом изогнутый под прямым углом конец трубки располагается в жидкости так, чтобы ось нижнего колена совпадала с линией тока. В трубке Пито создается дополнительное давление от воздействия скорости движущейся жидкости (скоростной напор).
Измерение скорости в потоке закрытого трубопровода можно провести по разности показаний трубки Пито , определяющей полный напор h1=((p/rg)+v2/(2g)), и пьезометрической трубки, определяющей пьезометрический напор – h2=p/rg. Скорость потока (м/с) в точке расположения нижнего отверстия трубки Пито можно определить по высоте подъема жидкости h3= v2/(2g).
 |
Применяя уравнение Бернулли к случаю истечения жидкости через малое отверстие при постоянном напоре, получаем выражение для расхода жидкости, известное как формула Торричелли:
где m — коэффициент расхода (истечения), который определяется экспериментально и зависит от вида (формы) отверстия; f — площадь поперечного сечения отверстия; h — напор.
Учитывая, что напор h=p/(rg), формулу Торичелли преобразуем к виду

где Δp — перепад давления в отверстии.
Эту формулу часто используют для расчета процессов дросселирования, прохождения жидкости через местное гидравлическое сопротивление (золотники, клапаны и другие гидроаппараты).

3.9. Виды потоков жидкости
Различают два вида течения жидкости в различных условиях: струйное и вихревое. Струйное течение называют ламинарным, а вихревое — турбулентным.
Режим течения оценивается числом Рейнольдса
 ,
,
где v — средняя скорость потока, м/с; n — кинематическая вязкость, м2/с; d — гидравлический диаметр; при круглом сечении он соответствует внутреннему диаметру трубы, м; в других случаях его необходимо определять по выражению

 .
.
Здесь: S — площадь сечения, м2; L — смоченный периметр сечения, м.
Число Рейнольдса - Re является безразмерным. При критическом значении Rекр поток переходит из ламинарного режима в турбулентный. Для жестких гладких круглых труб Rекр равно 2300, для гибких рукавов 1600, для гладких кольцевых щелей 1000…1100, для окон цилиндрических золотниковых распределителей 260, для кранов 550…750. Критическое значение Rекр определяет точку, ниже которой гарантированно не может существовать турбулентный режим течения.
Рассмотрим различные течения жидкости в терминах энергетического спектра и в пространстве состояний, если поместить какое-либо тело в поток жидкости, например, опору моста в русло реки, то при очень малых скоростях жидкость течёт ламинарно (рис.3.8). Такое течение является стационарным, т.е. скорость в любой точке пространства не зависит от времени. Следовательно вся энергия в спектре сосредоточена на нулевой частоте. В пространстве состояний такое течение изображается одной точкой. Эта точка является устойчивой траекторией системы т.е. если начальное течение соответствовало другой точке в пространстве состояний, то в пределе любое распределение скоростей будет стремится к устойчивому. (Строго говоря не любое, а любое из области притяжения устойчивой траектории). С ростом скорости в 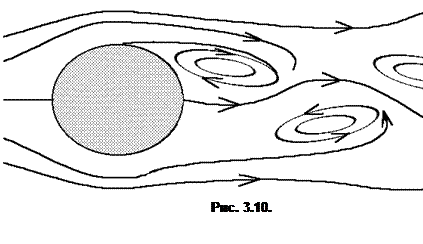
потоке образуются вихри, однако картина продолжает оставаться стационарной (рис. 3.9.). Так как поле скоростей по прежнему стационарно, то никаких изменений относительно ламинарного течения в спектре не произойдёт. В пространстве состояний это течение будет так же, как и ламинарное изображаться одной точкой, однако, её положение изменится. При дальнейшем росте скорости возможен отрыв вихрей и их увлечение потоком. Возникает нестационарное течение, которое, например, можно наблюдать с моста. При этом скорость, измеренная в некоторой точке вниз по потоку за мостом, оказывается периодической функцией времени (рис.3.10.). В такой ситуации происходит качественное изменение как энергетического спектра, так и траектории системы в пространстве состояний. В спектре появляется новая частота отличная от нулевой, а траектория в пространстве состояний из точки превращается в устойчивый цикл. В одном из первых сценариев возникновения турбулентности --- сценарии Ландау --- предполагалось, что по мере увеличения числа Рейнольдса в системе будет возникать всё больше новых частот. Траектория системы будет усложнятся: предельный цикл превратится в двумерный тор, этот тор в свою очередь превратится в трёхмерный и далее бесконечный каскад новых торов. Однако, сейчас не вызывает сомнений, что в большинстве систем сценарий возникновения турбулентности другой и данный сценарий крайне маловероятен. Один из сценариев имеющих экспериментальное подтверждение будет рассмотрен далее. При ещё большем возрастании числа Рейнольдса крупные вихри начинают порождать неупорядоченные внутренние вихри. В зависимости скорости от времени кроме периодической компоненты, появляются так же и нерегулярные отклонения. Спектр 
пред
 |
ставляет собой пики основных частот на фоне сравнительно малоинтенсивного «белого шума». Траектория системы начинает размываться. Она совершает нерегулярные колебания небольшой амплитуды около некоторого тора. В этом случае мы наблюдаем следующую картину потока (рис. 3.11.). Если число Рейнольдса возрастёт ещё больше, то возникает чрезвычайно сложное поле скоростей, и траектория системы, становится совершенно хаотической. Непосредственно за телом возникает, так называемый, турблентный след. Из спектра исчезают пики частот и возрастает интенсивность шума. Шум практически равномерно распределён в довольно широком интервале частот. Картина потока соответствующая такой ситуации изображена на рис. 3.12. Полной теории, исчерпывающим образом объясняющей возникновение турбулентности в различных типах гидродинамических течений, на сегодняшний день не существует.
Сопротивление течению жидкости увеличивается, гидравлические потери повышаются.
Дата добавления: 2015-04-18; просмотров: 390; Мы поможем в написании вашей работы!; Нарушение авторских прав |