Теорема Хеза.

Теорема (Хеза). Пусть является отношением, и 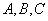- атрибуты или множества атрибутов этого отношения. Если имеется функциональная зависимость , то проекци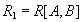и и образуют декомпозицию без потерь.

Доказательство. Необходимо доказать, что для любого состояния отношения . В левой и правой части равенства стоят множества кортежей, поэтому для доказательства достаточно доказать два включения для двух множеств кортежей: и .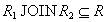

Докажем первое включение. Возьмем произвольный кортеж 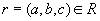. Докажем, что он включается также и в 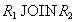. По определению проекции, кортеж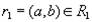и и 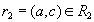. По определению естественного соединения кортеж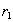и и 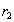, имеющие одинаковое значение 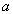общего атрибута 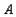, будут соединены в процессе естественного соединения в кортеж 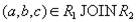. Таким образом, включение доказано.

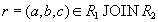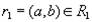Докажем обратное включение. Возьмем произвольный кортеж . Докажем, что он включается также и в . По определению естественного соединения получим, что в имеются кортежи и 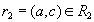. Т.к. 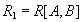, то существует некоторое значение 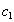, такое что кортеж 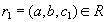. Аналогично, существует некоторое значение 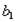, такое что кортеж 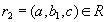. Кортеж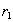и и имеют одинаковое значение атрибута 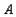, равное 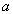. Из этого, в силу функциональной зависимости , следует, что 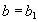. Таким образом, кортеж . Обратное включение доказано. Теорема доказана.

Замечание. В доказательстве теоремы Хеза наличие функциональной зависимости не использовалось при доказательстве включения . Это означает, что при выполнении декомпозиции и последующем восстановлении отношения при помощи естественного соединения, кортежи исходного отношения не будут потеряны. Основной смысл теоремы Хеза заключается в доказательстве того, что при этом не появятся новые кортежи, отсутствовавшие в исходном отношении.

Т.к. алгоритм нормализации (приведения отношений к 3НФ) основан на имеющихся в отношениях функциональных зависимостях, то теорема Хеза показывает, что алгоритм нормализации является корректным, т.е. в ходе нормализации не происходит потери информации.

НФБК

Определение 1. Отношение находится в нормальной форме Бойса-Кодда (НФБК) тогда и только тогда, когда детерминанты всех функциональных зависимостей являются потенциальными ключами.

Замечание. Если отношение находится в НФБК, то оно автоматически находится и в 3НФ. Действительно, это сразу следует из определения 3НФ.

Пример . Предположим, что нам необходимо учитывать поставки, но каждый акт поставки должен иметь некоторый уникальный номер (назовем его "сквозной номер поставки"). Отношение может иметь следующий вид:

Одним потенциальным ключом данного отношения является, пара атрибутов {PNUM, DNUM}. Другим ключом, в силу уникальности сквозного номера, является атрибут NN. В данном отношении имеются следующие функциональные зависимости: Зависимость атрибутов от первого ключа отношения:

{PNUM, DNUM} 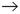VOLUME, {PNUM, DNUM} 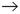NN, Зависимость атрибутов от второго ключа отношения: NN 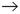PNUM, NN 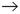DNUM, NN 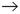VOLUME,

Зависимости, являющиеся следствием зависимостей от ключей отношения:

{PNUM, DNUM} 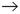{VOLUME, NN}, NN 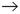{PNUM, DNUM}, NN 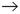{PNUM, VOLUME}, NN 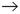{DNUM, VOLUME}, NN 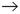{PNUM, DNUM, VOLUME}.

детерминанты всех зависимостей являются потенциальными ключами, поэтому данное отношение находится в НФБК. Особенностью данного отношения является то, что оно имеет два совершенно независимых потенциальных ключа.