Пятая нормальная форма.

Функциональные и многозначные зависимости позволяют произвести декомпозицию исходного отношения без потерь на две проекции. Можно, однако, привести примеры отношений, которые нельзя декомпозировать без потерь ни на какие две проекции.

Определение 5. Пусть является отношением, а 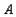, , …, 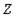- произвольными (возможно пересекающимися) подмножествами множества атрибутов отношения . Тогда отношение удовлетворяет зависимости соединения

тогда и только тогда, когда оно равносильно соединению всех своих проекций с подмножествами атрибутов 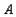, , …, , 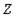т.е.

.

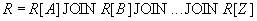Покажем, что зависимость соединения является обобщением понятия многозначной зависимости. Действительно, согласно теореме Фейджина, отношение может быть декомпозировано без потерь на проекции и 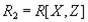тогда и только тогда, когда имеется многозначная зависимость . Согласно определению зависимости соединения, теорема Фейджина может быть переформулирована следующим образом:

Теорема Фейджина (другая формулировка). Отношение удовлетворяет зависимости соединения тогда и только тогда, когда имеется многозначная зависимость .

Т.к. теорема Фейджина является взаимно обратной, то ее можно взять в качестве определения многозначной зависимости. Таким образом, многозначная зависимость является частным случаем зависимости соединения, т.е., если в отношении имеется многозначная зависимость, то имеется и зависимость соединения. Обратное, конечно, неверно.

Определение 6. Зависимость соединения называется нетривиальной зависимостью соединения, если выполняется два условия:

· Одно из множеств атрибутов не содержит потенциального ключа отношения .

· Ни одно из множеств атрибутов не совпадает со всем множеством атрибутов отношения .

Для удобства работы сформулируем это определение так же и в отрицательной форме:

Определение 7. Зависимость соединения называется тривиальной зависимостью соединения, если выполняется одно из условий:

· Либо все множества атрибутов содержат потенциальный ключ отношения .

· Либо одно из множеств атрибутов совпадает со всем множеством атрибутов отношения .

Определение 8. Отношение находится в пятой нормальной форме (5НФ) тогда и только тогда, когда любая имеющаяся зависимость соединения является тривиальной.

Определения 5НФ может стать более понятным, если сформулировать его в отрицательной форме:

Определение 9. Отношение не находится в 5НФ, если в отношении найдется нетривиальная зависимость соединения.