Теорема Фейджина.

Теорема (Фейджина). Пусть , , 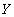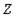- непересекающиеся множества атрибутов отношения .

Декомпозиция отношения на проекции и 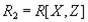будет декомпозицией без потерь тогда и только тогда, когда имеется многозначная зависимость .

Замечание. Если зависимость является тривиальной, т.е. существует одна из функциональных зависимосте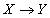й или 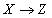, то получаем теорему Хеза.

Доказательство теоремы.

Необходимость. Пусть декомпозиция отношения на проекции и 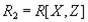является декомпозицией без потерь. Докажем что .

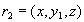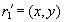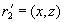Предположим, что отношение содержит кортежи и . Необходимо доказать, что кортеж также содержится в . По определению проекций, кортеж содержится в , а кортеж содержится в 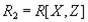. Тогда кортеж содержится в естественном соединении 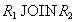, а в силу того, что декомпозиция является декомпозицией без потерь, этот кортеж содержится и в . Необходимость доказана.

Достаточность. Пусть имеется многозначная зависимость . Докажем, что декомпозиция отношения на проекции и 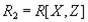является декомпозицией без потерь.

Как и в доказательстве теоремы Хеза, нужно доказать, что для любого состояния отношения .

Включение доказывается как в теореме Хеза. Такое включение выполняется всегда для любой декомпозиции отношения .

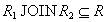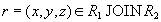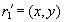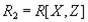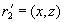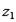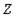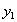Докажем включение . Пусть кортеж . Это означает, что в проекции содержится кортеж , а в проекции содержится кортеж . По определению проекции, найдется такое значение атрибута , что отношение содержит кортеж . Аналогично, найдется такое значение атрибута 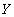, что отношение содержит кортеж 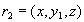. Тогда по определению многозначной зависимости кортеж . Включение доказано. Достаточность доказана. Теорема доказана.