
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Многозначные зависимости.
Определение 2. Пусть  - отношение, и
- отношение, и  ,
, 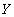 ,
, 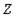 - некоторые из его атрибутов (или непересекающиеся множества атрибутов). Тогда атрибуты (множества атрибутов)
- некоторые из его атрибутов (или непересекающиеся множества атрибутов). Тогда атрибуты (множества атрибутов) 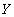 и
и 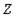 многозначно зависят от
многозначно зависят от  (обозначается
(обозначается  ), тогда и только тогда, когда из того, что в отношении
), тогда и только тогда, когда из того, что в отношении  содержатся кортежи
содержатся кортежи  и
и 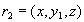 следует, что в отношении
следует, что в отношении  содержится также и кортеж к
содержится также и кортеж к  . Замечание. Меняя местами кортежи
. Замечание. Меняя местами кортежи 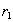 и
и  в определении многозначной зависимости, получим, что в отношении
в определении многозначной зависимости, получим, что в отношении  должен содержаться также и кортеж
должен содержаться также и кортеж 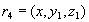 . Таким образом, атрибуты
. Таким образом, атрибуты 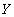 и
и 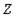 , многозначно зависящие от
, многозначно зависящие от  , ведут себя "симметрично" по отношению к атрибуту
, ведут себя "симметрично" по отношению к атрибуту  .
.
В отношении "Абитуриенты-Факультеты-Предметы" имеется многозначная зависимость Факультет  Абитуриент|Предмет. Словами это можно выразить так - для каждого факультета (для каждого значения из
Абитуриент|Предмет. Словами это можно выразить так - для каждого факультета (для каждого значения из  ) каждый поступающий на него абитуриент (значение из
) каждый поступающий на него абитуриент (значение из 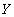 ) сдает один и тот же список предметов (набор значений из
) сдает один и тот же список предметов (набор значений из 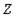 ), и для каждого факультета (для каждого значения из
), и для каждого факультета (для каждого значения из  ) каждый сдаваемый на факультете экзамен (значение из
) каждый сдаваемый на факультете экзамен (значение из 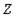 ) сдается одним и тем же списком абитуриентов (набор значений из
) сдается одним и тем же списком абитуриентов (набор значений из 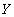 ). Именно наличие этой зависимости не позволяет независимо вставлять и удалять кортежи. Кортежи обязаны вставляться и удаляться одновременно целыми наборами. Замечание. Если в отношении
). Именно наличие этой зависимости не позволяет независимо вставлять и удалять кортежи. Кортежи обязаны вставляться и удаляться одновременно целыми наборами. Замечание. Если в отношении  имеется не менее трех атрибутов
имеется не менее трех атрибутов  ,
, 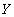 ,
, 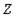 и есть функциональная зависимость
и есть функциональная зависимость 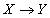 , то есть и многозначная зависимость
, то есть и многозначная зависимость  . Действительно, действуя формально в соответствии с определением многозначной зависимости, предположим, что в отношении
. Действительно, действуя формально в соответствии с определением многозначной зависимости, предположим, что в отношении  содержатся кортежи
содержатся кортежи  и
и 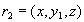 . В силу функциональной зависимости
. В силу функциональной зависимости 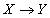 отсюда следует, что
отсюда следует, что 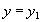 . Но тогда кортеж
. Но тогда кортеж  в точности совпадает с кортежем
в точности совпадает с кортежем 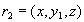 и, следовательно, содержится в отношении
и, следовательно, содержится в отношении  . Таким образом, имеется многозначная зависимость
. Таким образом, имеется многозначная зависимость  . Таким образом, понятие многозначной зависимости является обобщением понятия функциональной зависимости. Определение 3. Многозначная зависимость
. Таким образом, понятие многозначной зависимости является обобщением понятия функциональной зависимости. Определение 3. Многозначная зависимость  называется нетривиальной многозначной зависимостью, если не существует функциональных
называется нетривиальной многозначной зависимостью, если не существует функциональных
Дата добавления: 2015-04-18; просмотров: 287; Мы поможем в написании вашей работы!; Нарушение авторских прав |