
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методические требования к использованию коэффициента корреляции
- измерение связи возможно только в качественно однородных совокупностях (например, измерение связи между ростом и весом в совокупностях, однородных по полу и возрасту)
- расчет может производиться с использованием абсолютных или производных величин
- для вычисления коэффициента корреляции используются не сгруппированные вариационные ряды (это требование применяется только при вычислении коэффициента корреляции по методу квадратов)
- число наблюдений менее 30
22. Методы выявления тенденции в ряду динамики
Одной из задач, возникающих при анализе рядов динамики, является установление закономерности изменения уровней изучаемого показателя во времени. Для этого необходимо выделить такие периоды (этапы) развития, которые достаточно однородны в отношении взаимосвязи данного явления с другими и условий его развития.
Выделение этапов развития – это задача, находящаяся на стыке науки, изучающей данное явление (экономики, социологии и т. п.), и статистики. Решение этой задачи осуществляется не только и даже не столько с помощью статистических методов (хотя и они могут принести определенную пользу), сколько на базе содержательного анализа сущности, природы явления и общих законов его развития.
Для каждого этапа развития нужно выявить и численно охарактеризовать основную тенденцию изменения уровня явления. Под тенденциейпонимается общее направление к росту, снижению или стабилизации уровня явления с течением времени. Если уровень непрерывно растет или непрерывно снижается, то тенденция к росту или снижению наблюдается отчетливо: она легко обнаруживается визуально по графику временного ряда. Следует, однако, иметь в виду, что и рост, и снижение уровня могут происходить по-разному: либо равномерно, либо ускоренно, либо замедленно. Под равномерным ростом(или снижением) понимается рост (или снижение) с постоянной абсолютной скоростью, когда цепные абсолютные приросты (;) одинаковы. При ускоренном ростеили снижении цепные приросты систематически увеличиваются по абсолютной величине, а при замедленном ростеили снижении – уменьшаются (тоже по модулю). Практически уровни ряда динамики очень редко растут (или снижаются) строго равномерно. Нечасто встречается и систематическое, без единого отклонения, увеличение или снижение цепных приростов.
Такие отклонения объясняются либо изменением с течением времени всего комплекса основных причин и факторов, от которых зависит уровень явления, либо изменением направления и силы действия второстепенных, в том числе случайных, обстоятельств и факторов, поэтому при анализе динамики идет речь не просто о тенденции развития, а об основной тенденции, достаточно стабильной (устойчивой) на протяжении данного этапа развития. В некоторых случаях эта закономерность, общая тенденция развития объекта вполне четко отображаются уровнями динамического ряда.
Основной тенденцией (трендом)называется достаточно плавное и устойчивое изменение уровня явления во времени, более или менее свободное от случайных колебаний. Основную тенденцию можно представить либо аналитически – в виде уравнения (модели) тренда, либо графически. Выявление основной тенденции развития (тренда) называется в статистике также выравниваем временного ряда,а методы выявления основной тенденции – методами выравнивания.
Одними из самых распространенных способов выявления основных тенденций (тренда) ряда динамики являются методы:
• укрупнения интервалов;
• скользящей средней (суть метода состоит в замене абсолютных данных средними арифметическими за определенные периоды). Расчет средних ведется способом скольжения, т. е. постепенным исключением из принятого периода первого уровня и включение следующего;
• аналитического выравнивания. При этом уровни ряда динамики выражаются в виде функций времени:
1) f (t) = a0 + a1t – линейная зависимость;
2) f(t) = a0 + a1t + a2t2– параболическая зависимость. Способ укрупнения интервалови их характеристики средними уровнями заключается в переходе от интервалов менее продолжительных к более продолжительным, например от суток – к неделям или декадам, от декад – к месяцам, от месяцев – к кварталам или годам, от годовых интервалов – к многолетним. Если уровни ряда динамики колеблются с более или менее определенной периодичностью (волнообразно), то укрупненный интервал целесообразно взять равным периоду колебаний (длине «волны» цикла). Если же такая периодичность отсутствует, то укрупнение производят постепенно от малых интервалов к все более крупным, пока общее направление тренда не станет достаточно отчетливым.
Если ряд динамики является моментным, а также в тех случаях, когда уровень ряда является относительной или средней величиной, суммирование уровней не имеет смысла, и следует охарактеризовать укрупненные периоды средними уровнями.
При укрупнении интервалов число членов динамического ряда сильно сокращается, в результате чего движение уровня внутри укрупненного интервала выпадает из поля зрения. В связи с этим для выявления основной тенденции и более детальной ее характеристики используется сглаживание ряда с помощью скользящей средней.
Сглаживание ряда динамики с помощью скользящей среднейзаключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем – средний уровень из такого же числа уровней, начиная со второго, далее, начиная с третьего и т. д. Таким образом, при расчетах среднего уровня как бы «скользят» по временному ряду от его начала к концу, каждый раз отбрасывая один уровень в начале и добавляя один следующий. Отсюда название – скользящая средняя.
Каждое звено скользящей средней – это средний уровень за соответствующий период. При графическом изображении и при некоторых расчетах каждое звено принято условно относить к центральному интервалу того периода, за который сделан расчет (для моментального ряда – к центральной дате).
Вопрос о том, за какой период следует вычислять звенья скользящей средней, решается в зависимости от конкретных особенностей динамики. Как и при укрупнении интервалов, если в колебаниях уровня есть определенная периодичность, то период сглаживания целесообразно принять равным периоду колебаний или кратной его величине. Так, при наличии квартальных уровней, испытывающих ежегодно сезонные спады и повышения, целесообразно применять четырех– или восьмиквартальную среднюю и т. п. Если же колебания уровней являются беспорядочными, то целесообразно постепенно укрупнять интервал сглаживания, пока не выявится отчетливая картина тренда.
Аналитическое выравнивание ряда динамикипозволяет получить аналитическую модель тренда. Оно производится следующим образом.
• На основе содержательного анализа выделяется этап развития и устанавливается характер динамики на этом этапе.
• Исходя из предположения о той или иной закономерности роста и из характера динамики выбирается форма аналитического выражения тренда, вид аппроксимирующей функции, которой графически соответствует определенная линия: прямая, парабола, показательная кривая и т. п. Эта линия (функция) выражает предполагаемую закономерность плавного изменения уровня во времени, т. е. основную тенденцию. При этом каждый уровень ряда динамики условно рассматривается как сумма двух составляющих (компонент): yt=f(t)+?t. Одна из них (yt = f (t)), выражающая тренд, характеризует влияние постоянно действующих, основных факторов и называется систематический регулярной компонентой.Другая составляющая (8t) отражает влияние случайных факторов и обстоятельств и называется случайной компонентой.Эту компоненту называют также остаточной(или просто остатком), так как она равна отклонению фактического уровня от тренда. Таким образом, допускается (условно предполагается), что основная тенденция (тренд) формируется под влиянием постоянно действующих главных факторов, а второстепенные, случайные факторы вызывают отклонение уровня от тренда.
Выбор формы кривой во многом определяет результаты экстраполяции тренда. Основанием для выбора вида кривой может использоваться содержательный анализ сущности развития данного явления. Можно опираться также на результаты предыдущих исследований в данной области. Наиболее простой эмпирический прием – визуальный: выбор формы тренда на основе графического изображения ряда – ломаной линии. На практике линейная зависимость используется чаще, чем параболическая, в силу ее простоты.
23. Методы измерения связей между количественными (варьирующими) признаками
24. Методы определения средней численности населения
Лекции!
25. Методы расчета валового внутреннего продукта. Основные схемы счетов
26. Методы, виды и способы отбора выборочных совокупностей
виды выборочного наблюдения:
собственно-случайная;
типическая;
серийная;
механическая;
Собственно-случайная - есть отбор единиц из генеральной совокупности путем случайного отбора, но при условии вероятности выбора любой единицы из генеральной совокупности. Отбор проводится методом жеребьевки или по таблице случайных чисел.
Типическая выборка предполагает разделение неоднородной генеральной совокупности на типологические или районированные группы по какому-либо существенному признаку, после чего из каждой группы производится случайный отбор единиц.
Для серийной выборки характерно то, что генеральная совокупность первоначально разбивается на определенные равновеликие или неравновеликие серии (единицы внутри серий связаны по определенному признаку), из которых путем случайного отбора отбираются серии и затем внутри отобранных серий проводится сплошное наблюдение.
Механическая выборка представляет собой отбор единиц через равные промежутки (по алфавиту, через временные промежутки, по пространственному способу и т.д.). При проведении механического отбора генеральная совокупность разбивается на равные по численности группы, из которых затем отбирается по одной единице.
27.Организационные формы, виды и способы статистического наблюдения
Формы статистического наблюдения. В отечественной статистике используются три организационные формы статистического наблюдения:
• Отчетность (предприятий, организаций, учреждений и т.п.) - основная форма статистического наблюдения, с помощью которой статистические органы в определенные сроки получают от предприятий, учреждений необходимые данные в виде установленных отчетных документов..
• Специально организованное статистическое наблюдение. Ярким примером является перепись – специально организованная отчетность, которая повторяется через равные промежутки времени с целью получения данных о численности, составе и состоянии объекта по ряду признаков.
Особенности переписи:
- одновременностьее проведения на всей территории страны
- единство программы статистического наблюдения
• Регистр- система, постоянно следящая за состоянием единицы наблюдения и оценивающую силу воздействия различных факторов на изучаемые показатели.
Регистр населения – поименованный и регулярно изменяемый перечень жителей страны. В данном случае программа наблюдения ограниченна общими признаками (пол, дата и место рождения, дата вступления в брак).
Регистр предприятий, который включает в себя все виды экономической деятельности. Содержит данные о времени создания или регистрации предприятий, название, адрес, телефон, организационно-правовую форму, вид экономической деятельности, количество занятых и т.д., т.е. полную информацию о предприятии.
28. Организация системы государственной статистики на современном этапе
В настоящее время центральным органом системы государственной статистики является Государственный комитет Российской Федерации по статистике (Госкомстат России).
Единую систему государственной статистики Российской Федерации при Госкомстате России составляют органы в республиках, автономных областях и округах, краях, городах и районах.
Мощными вычислительными ресурсами обладает Главный межрегиональный центр обработки и распространения статистической информации. Этот центр необходим для обработки поступающих из регионов статистических данных.
Основная деятельность Госкомстата– это разработка федеральных статистических программ, финансируемых из госбюджета.
Основные задачи Госкомстата:
1) координация статистической деятельности в государстве;
2) разработка статистической методологии
3) предоставление официальной статистической информации Президенту, Правительству, общественности, Федеральному Собранию Российской Федерации, федеральным органам исполнительной власти, международным и иным организациям.
определенные виды статистических работ ведутся не только Госкомстатом России, но и иными органами государственного управления: Банком России, Министерством образования России, МинФин, Министерством труда России, МВД.
29. Закон больших чисел
Главным обобщением опыта исследования любых массовых явлений служат закон больших чисел. Отдельное единичное явление, рассматриваемое как одно из явлений данного рода, содержит в себе элемент случайного: оно могло быть или не быть, быть таким или иным. При соединении же большого числа таких явлений в общих характеристиках всей их массе случайность исчезает в тем большей мере, чем больше соединено единичных явлений.
Математика, в частности теория вероятностей, рассматриваемая в чисто количественном аспекте закон больших чисел, выражает его целой цепью математических теорем. Они показывают, при каких условиях и в какой именно мере можно рассчитывать на отсутствие случайности в охватывающих массу характеристиках, как это связано с численностью входящих в них индивидуальных явлений. Статистика же основывается на этих теоремах в изучении каждого конкретного массового явления.
Закономерность, проявившаяся лишь в большой массе явлений через преодоление свойственной ее единичным элементам случайности, называется статистической закономерностью.
В одних случаях перед статистикой стоит задача измерения ее проявлений, само же ее существование теоретически ясно заранее.
В других случаях закономерность может быть найдена статистикой эмпирически. Этим путем было, например, установлено, что с увеличением дохода семьи в ее бюджете падает процент расходов на питание.
Таким образом всякий раз, когда статистика в исследовании какого-либо явления достигает обобщений и находит действующую в нем закономерность, эта последняя сразу становится достоянием той конкретной науки, к кругу интересов которой принадлежит это явление. Следовательно, в отношении каждой статистика выступает в качестве метода.
Рассматривая результаты массового наблюдения , статистика находит в них черты сходства и различия, соединяет элементы в группы, выявляя при этом различные типы, дифференцируя по этим типам всю подвергнутую наблюдению массу. Результаты наблюдения единичных элементов массы используются, далее для получения характеристик всей совокупности и выделенных в ней особых частей, т.е. для получения обобщающих показателей.
Массовое наблюдение, группировка и сводка его результатов, вычисление и анализ обобщающих показателей – таковы главные черты метода статистики.
Статистика как наука опекает и сводится к математической статистике. В математике задачи характеристики массовых явлений рассматриваются только в чисто количественном аспекте, оторванно от качественного содержания (что обязательно для математики, как науки вообще). Статистика же даже в исследовании общих законов массовых явлений исходит не только из количественных обобщений этих явлений, а прежде всего из механизма возникновения самого массового явления.
В тоже время из сказанного о роли количественного измерения для статистики следует большое значение для нее математических методов вообще, специально приспособленных для решения задач, возникающих при исследовании массовых явлений (теория вероятностей и математической статистики). Более того, роль математических методов здесь настолько велика, что попытка их исключения из курса статистики (ввиду наличия в планах отдельного предмета – математической статистики) существенно обедняет статистику.
Отказ от этой попытки, однако, не должен означать противоположной крайности, а именно поглощения статистикой всей теории вероятностей и математической статистики. Если, например, в математике рассматривается средняя величина для ряда распределения (вероятностей или эмпирических частостей),то статистика так же не может обойти соответствующие приемы, но здесь это один из аспектов, наряду с которым возникает и ряд других (средние общие и групповые, возникновение и роль средних в системе информации, материальное содержание системы весов, хронологические средние, средние и относительные величины и т.д.).
Или другой пример: математическая теория выборки все внимание сосредоточивает на ошибке репрезентативности – для разных систем отбора, разных характеристик и т.д. Системную ошибку, т.е. ошибку не поглощающуюся в средней величине, она заранее исключает, строя свободные от нее так называемые несмещенные оценки. В статистике же едва ли не главным в этом деле вопросом является вопрос о том, как эту системную ошибку избежать.
В исследовании количественной стороны массовых явлений возникает ряд задач математического характера. Для их решения математика разрабатывает соответствующие приемы, но для этого она должна рассматривать их в общем виде, для которого качественное содержание массового явления безразлично. Так проявление закона больших чисел было впервые подмечено именно в социально-экономической области и почти одновременно в азартных играх (само распределение которых объяснилось тем, что они являлись слепком с экономики, в частности развивающихся товарно-денежных отношений). С того момента, однако, когда закон больших чисел становится объектом точного исследования в математике, он получает совершенно общую трактовку, которая не ограничивает его действие какой-либо специальной областью.
На этом основании предмет статистики вообще отграничивается от предмета математики. Разграничения объектов не может означать изгнать из одной науки всего, что попало в поле зрения другой. Было бы, например, неправильно исключить из изложения физики всего связанного с применением дифференциальных уравнений на том основании, что ими занимается математика.
30. Относительные показатели, характеризующие рынок труда
31. Ошибки выборочного наблюдения и определение необходимой численности выборки
Под ошибкой репрезентативности понимают расхождение между выборочной характеристикой и предполагаемой характеристикой генеральной совокупности.
Ошибки репрезентативности бывают случайными и систематическими.
Систематические ошибки связаны с нарушением установленных правил отбора.
Случайные ошибки объясняются недостаточно равномерным представлением в выборочной совокупности различных категорий единиц генеральной совокупности.
В результате первой причины (систематические ошибки) выборка легко может оказаться смещенной, так как при отборе каждой единицы допускается ошибка, всегда направленная в одну и ту же сторону. Эта ошибка получила название ошибки смещения. Ее размер может превышать величину случайной ошибки. Особенность ошибки смещения состоит в том, что, представляя собой постоянную часть ошибки репрезентативности, она увеличивается с увеличением объема выборки. Случайная же ошибка с увеличением объема выборки уменьшается. Кроме того, величину случайной ошибки можно определить, в то время как размер ошибки смещения непосредственно практически определить очень сложно, а иногда и невозможно. Поэтому важно знать причины, вызывающие ошибку смещения, и предусмотреть мероприятия по ее устранению.
Ошибки смещения бывают преднамеренными и непреднамеренными. Причиной возникновения преднамеренной ошибки является тенденциозный подход к выбору единиц из генеральной совокупности. Чтобы не допустить появления такой ошибки, необходимо соблюдать принцип случайности отбора единиц.
Непреднамеренные ошибки могут возникать на стадии подготовки выборочного наблюдения, формирования выборочной совокупности и анализа ее данных. Чтобы не допустить появления таких ошибок, необходима хорошая основа выборки, т. е. та генеральная совокупность, из которой предполагается производить отбор, например список единиц отбора. Основа выборки должна быть достоверной, полной и соответствовать цели исследования, а единицы отбора и их характеристики должны соответствовать действительному их состоянию на момент подготовки выборочного наблюдения. Нередки случаи, когда в отношении некоторых единиц, попавших в выборку, трудно собрать сведения из-за их отсутствия на момент наблюдения, нежелания дать сведения и т. п. В таких случаях эти единицы приходится заменять другими. Необходимо следить, чтобы замена осуществлялась равноценными единицами.
Случайная ошибка выборки возникает в результате случайных различий между единицами, попавшими в выборку, и единицами генеральной совокупности, т. е. она связана со случайным отбором. Теоретическим обоснованием появления случайных ошибок выборки являются теория вероятностей и ее предельные теоремы.
Так, для случайного повторного объема выборки (n) имеем:
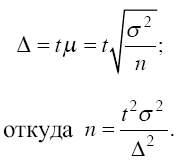
Суть этой формулы – в том, что при случайном повторном отборе необходимой численности объем выборки прямо пропорционален квадрату коэффициента доверия (t2)и дисперсии вариационного признака (?2)и обратно пропорционален квадрату предельной ошибки выборки (?2).
32. Платежный баланс
Платежный баланс — статистический отчет, в котором отражаются все внешнеэкономические операции за определенный период (обычно за квартал, полугодие, год) между резидентами данной страны и остальным миром. Он отражает также операции с иностранными активами между отечественными секторами экономики. Платежный баланс — один из основных инструментов макроэкономического анализа прогнозирования и регулирования экономики в условиях рыночных отношений.
Задачи статистики платежного баланса состоят в том, чтобы разработать такую систему показателей, которая позволила:
§ охарактеризовать развитие внешней торговли страны за определенный отрезок времени, влияние на валютный курс, уровень производства, занятость и потребление;
§ показать, в каких масштабах и формах происходило привлечение иностранных инвестиций и осуществлялись инвестиции за границу;
§ ответить на вопрос, насколько своевременно осуществлялось погашение внешней задолженности страны, каковы размеры просрочки и характер ее реструктуризации;
§ оценить изменение уровня международных резервов Центрального банка с целью устранения платежных дисбалансов.
Данные платежного баланса используются для определения фискальной и монетарной политики, протекционистских мер, регулирования внутреннеговалютного рынка и валютного курса. Эти данные служат одним из информационных источников для составления СНС, таких важнейших экономических показателей, как ВВП и национальный доход.
Платежный баланс включает счет текущих операций, счет операций с капиталом и финансовый счет. Платежный баланс отражает операции, которые совершаются между резидентами и нерезидентами. К ним относятся операции с товарами (например, сельскохозяйственной продукцией, продукцией добывающей и обрабатывающей промышленности); услугами (транспортными, туристическими, строительными и др.); доходами (например дивидендами и процентами); трансфертами (например иностранной помощью) и финансами (кредитами и займами; наличными денежными средствами и депозитами; инвестициями в акции, облигации, краткосрочные финансовые инструменты, обращающиеся на рынках).
Платежный баланс построен на основе методологических принципов бухгалтерского учета: каждая операция отражается дважды — по кредиту одного счета и дебету другого, корреспондируемого с первым. Сумма всех кредитовых проводок должна совпадать с суммой дебетовых, а общее сальдо должно всегда равняться нулю. Однако на практике наблюдаются расхождения, связанные с тем, что данные, характеризующие разные стороны одних и тех же операций, относятся к разным источникам информации.
Вместе с тем платежный баланс существенно отличается от бухгалтерского баланса. Если в последнем регистрируются активы (виды использования капитала) и пассивы (источники финансовых ресурсов) на определенную дату, то в платежном балансе экономические операции определяются как экономический поток, который является результатом взаимодействия институциональных единиц и отражает создание, преобразование, обмен, передачу или исчезновение экономических ценностей (как в СНС).
Статистическая отчетность, в которой отражаются все финансовые активы и обязательства резидентов по отношению к нерезидентам по состоянию на определенную дату, называется международной инвестиционной позицией. В платежном балансе отражаются изменения в объеме активов или обязательств, которые произошли в результате операций.
33. Показатели естественного движения населения
Лекции!
34. Показатели и индексы себестоимости
35. Показатели механического движения населения
Лекции!
36. Показатели средней численности и движения работников
37. Показатели статистики оборотных средств
38. Показатели численности трудовых ресурсов
39. Понятие бюджетной классификации, ее состав
40. Понятие вариации и показатели ее размера
Лекции!
41. Понятие выборочного наблюдения и его преимущества
Выборочная совокупность - это часть объектов генеральной совокупности, от которых исследователь получает необходимые сведения (проводя, например, интервью), а затем экстраполирует (распространяет) полученные результаты на всю генеральную совокупность.
Выборочный метод имеет ряд преимуществ:
· меньше стоимость. Затраты на получение данных лишь относительно небольшой части всей совокупности меньше, чем при сплошной переписи.
· короче сроки. По тем же причинам данные выборочного обследования можно собрать и обобщить быстрее, чем при сплошной переписи. Это особенно важно, когда сведения нужны срочно.
· шире область применения. При некоторых видах обследований для сбора данных необходимо привлечь высококвалифицированный персонал или воспользоваться специальным оборудованием; как правило, и то и другое ограничено. В этих случаях сплошное обследование невозможно. Выборочные обследования имеют более широкую область применения и дают большую возможность получать сведения самого разнообразного характера
· больше достоверность. Это утверждение может показаться парадоксальным, однако... Если общий объем работы меньше, то можно привлечь более квалифицированный персонал, лучше его подготовить, более тщательно контролировать проведение обследования и обработку его результатов. Поэтому выборочное обследование может дать более достоверные сведения, чем соответствующее сплошное обследование.
42. Понятие государственных финансов, их состав
Лекции!
43. Понятие денежного обращения и денежной массы.
44. Понятие денежной базы и ее составляющие
45. Понятие и методы расчета производительности труда
46. Понятие индексов в статистике. Классификация индексов
Лекции!
47. Понятие налогов и сборов, их основные группировки
Лекции!
48. Понятие национального богатства. Состав элементов национального богатства
49. Понятие рядов динамики, их виды, основные элементы и требования к построению
Лекции!
50. Понятие системы национальных счетов, основные классификации и группировки
51. Понятие средних величин, их виды и способы расчета степенных средних
Средней величиной называется статистический показатель, который дает обобщенную характеристику варьирующего признака однородных единиц совокупности.
Величина средней дает обобщающую количественную характеристику всей совокупности и характеризует ее в отношении данного признака.
Так, например, средняя заработная плата дает обобщающую количественную характеристику состояния оплаты труда рассматриваемой совокупности работников. Кроме того, используя средние величины, имеется возможность сопоставлять различные информационные совокупности. Так, например, можно сравнивать различные организации по уровню производительности труда, а также по уровню фондоотдачи, материалоотдачи и по другим показателям.
Сущность средней заключается в том, что в ней взаимопогашаются случайные отклонения значений признака и учитываются изменения вызванные основным фактором.
Средние величины широко применяются в различных отраслях знаний. Особо важную роль они играют в экономике и статистике: при анализе, планировании, прогнозировании, при расчете нормативов и при оценке достигнутого уровня. Средняя всегда именованная величина и имеет ту же размерность, что и отдельная единица совокупности.
Дата добавления: 2015-04-18; просмотров: 222; Мы поможем в написании вашей работы!; Нарушение авторских прав |