Срок наблюдения – это время, в течение которого происходит заполнение статистических формуляров, т.е. время, необходимое для проведения массового сбора данных.

58. Прожиточный минимум и показатели статистики бедности населения

59. Регрессионный анализ

60. Система показателей денежной массы

61. Система показателей и методы статистического анализа налогов

Лекции!

62. Система показателей статистики государственных финансов и государственного бюджета

63. Способы распространения выборочных данных на генеральную совокупность

Характеристика генеральной совокупности на основе выборочных результатов – это конечная цель выборочного наблюдения.

Выборочный метод применяется для получения характеристик генеральной совокупности по определенным показателям выборки. В зависимости от целей исследования это осуществляется прямым пересчетом показателей выборки для генеральной совокупности или методом расчета поправочных коэффициентов.

Способ прямого пересчета в том, что при нем показатели выборочной доли w или средней х распространяются на генеральную совокупность с учетом ошибки выборки.

Способ поправочных коэффициентов применяется, когда целью выборочного метода является уточнение результатов сплошного учета. Данный способ используется при уточнении данных ежегодных переписей скота у населения.

64. Средние индексы

В зависимости от методологии расчета индивидуальных и сводных индексов различают средние арифметическиеи средние гармонические индексы.Другими словами, общий индекс, построенный на базе индивидуального индекса, принимает форму среднего арифметического или гармонического индекса, т. е. он может быть преобразован в средний арифметический и средний гармонический индексы.

Идея построения сводного индекса в виде средней величины из индивидуальных (групповых) индексов вполне объяснима: ведь сводный индекс является общей мерой, характеризующей среднюю величину изменения индексируемого показателя, и, конечно, его величина должна зависеть от величин индивидуальных индексов. А критерием правильности построения сводного индекса в форме средней величины (среднего индекса) является его тождественность агрегатному индексу.

Преобразование агрегатного индекса в средний из индивидуальных (групповых) индексов производится следующим образом: либо в числителе, либо в знаменателе агрегатного индекса индексируемый показатель заменяется его выражением через соответствующий индивидуальный индекс.Если такую замену сделать в числителе, то агрегатный индекс будет преобразован в средний арифметический, если же в знаменателе – то в средний гармонический из индивидуальных индексов.

Например, известен индивидуальный индекс физического объема iq = q1/q0и стоимость продукции каждого вида в базисном периоде (q0p0).Исходной базой построения среднего из индивидуальных индексов служит сводный индекс физического объема:

(агрегатная форма индекса Ласпейреса).

Из имеющихся данных непосредственно суммированием можно получить только знаменатель формулы. Числитель же может быть получен перемножением стоимости отдельного вида продукции базисного периода на индивидуальный индекс:

Тогда формула сводного индекса примет вид:

т. е. получим средний арифметический индекс физического объема, где весами служит стоимость отдельных видов продукции в базисном периоде.

Допустим, что в наличии имеется информация о динамике объема выпуска каждого вида продукции (г^) и стоимости каждого вида продукции в отчетном периоде (p1q1). Для определения общего изменения выпуска продукции предприятия в этом случае удобно воспользоваться формулой Пааше:

Числитель формулы можно получить суммированием величин q1P1,а знаменатель – делением фактической стоимости каждого вида продукции на соответствующий индивидуальный индекс физического объема продукции, т. е. делением: p1q1/iq, тогда:

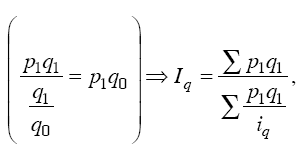
таким образом, получаем формулу среднего взвешенного гармонического индекса физического объема.

Применение той или иной формулы индекса физического объема (агрегатного, среднего арифметического и среднего гармонического) зависит от имеющейся в распоряжении информации. Также нужно иметь в виду, что агрегатный индекс может быть преобразован и рассчитан как средний из индивидуальных индексов только при совпадении перечня видов продукции или товаров (их ассортимента) в отчетном и базисном периодах, т. е. когда агрегатный индекс построен по сравнимому кругуединиц (агрегатные индексы качественных показателей и агрегатные индексы объемных показателей при условии сравнимого ассортимента).

65. Средние показатели ряда динамики

66. Статистика доходов населения

Лекции!

67. Статистика основных фондов. Оценка элементов национального богатства

68. Статистика расходов и потребления населения

69. Статистическая сводка, ее содержание и задачи

Научно организованная обработка материалов статистического наблюдения по заранее разработанной программе включает в себя систематизацию, группировку данных, составление таблиц, получение итогов и производных показателей (средних и относительных величин) и т. д. Собранный в процессе статистического наблюдения материал представляет собой разрозненные первичные сведения об отдельных единицах изучаемого явления.

Сводка представляет собой комплекс последовательных действий по обобщению конкретных единичных данных, образующих совокупность, с целью обнаружения типичных черт и закономерностей, присущих изучаемому явлению в целом.

Статистическая сводка в узком смысле слова (простая сводка) представляет собой операцию по подсчету общих итоговых (суммарных) данных по совокупности единиц наблюдения.

Статистическая сводка в широком смысле слова (сложная сводка) включает в себя также группировку данных наблюдения, подсчет общих и групповых итогов, получение системы взаимосвязанных показателей, представление результатов группировки и сводки в виде статистических таблиц.

Правильная, научно организованная сводка, опираясь на предварительный глубокий теоретический анализ, позволяет получить все статистические итоги, отражающие важнейшие, характерные черты объекта исследования, измерить влияние различных факторов на результат и учесть все это в практической работе при составлении текущих и перспективных планов.

Задача сводки – дать характеристику объекту исследования с помощью систем статистических показателей, выявить и измерить таким путем его существенные черты и особенности. Эта задача решается на трех этапах:

1. определение групп и подгрупп;

2. определение системы показателей;

3. определение видов таблиц.

На первом этапе осуществляется систематизация, группировка материалов, собранных при наблюдении. На втором этапе уточняется предусмотренная планом система показателей, с помощью которых количественно характеризуются свойства и особенности изучаемого предмета. На третьем этапе исчисляются сами показатели, и обобщенные данные для наглядности и удобства представляются в таблицах, статистических рядах, графиках, диаграммах.

Программа статистической сводки содержит перечень групп, на которые целесообразно расчленить совокупность, их границы в соответствии с группировочными признаками; систему показателей, характеризующих совокупность, и методику их расчета; систему макетов разработочных таблиц, в которых будут представлены итоги расчетов.

Наряду с программой существует план проведения сводки, который предусматривает ее организацию. План проведения сводки должен содержать указания о последовательности и сроках выполнения ее отдельных частей, об ответственных за ее выполнение, о порядке изложения результатов, а также предусматривать координацию работы всех организаций, задействованных в ее проведении.

70. Статистические ряды распределения, их виды

Статистический ряд распределения – это упорядоченное распределение единиц совокупности на группы по определенному варьирующему признаку.

В зависимости от признака, положенного в основу группировки различают атрибутивные и вариационные ряды распределения.

Атрибутивными называют ряды, построенные по качественным признакам.

Вариационными рядами называют ряды распределения, построенные по количественному признаку. Каждый вариационный ряд состоит из двух элементов: вариантов и частот. Вариантами считаются отдельные значения признака, которые он принимает в вариационном ряду, т.е. конкретное значение варьирующего признака. Частоты – это численности отдельных вариантов или каждой группы вариационного ряда, показывающие, как часто встречается та или иная варианта в ряду. Частостяминазывают частоты, выраженные в процентах или долях единицы.

В зависимости от характера вариации признака различают дискретные и интервальные вариационные ряды. В случае дискретной вариации величина количественного признака принимает только целые значения. В случае непрерывной вариации величина признака у единиц совокупности может принимать в определенных пределах любые значения.

71. Статистический анализ оборачиваемости денежной массы

72. Структура денежной массы и ее виды

Денежная масса представляет собой совокупность наличных и безналичных платежных средств, обеспечивающих обращение товаров и услуг в стране в определенный момент.

Ликвидность – способность быстрого перевода актива в наличные деньги без потерь его стоимости либо с минимальными издержками. Деньги (монеты и бумажные деньги) являются наиболее ликвидными активами. Банковские депозиты до востребования также являются высоколиквидными активами, поскольку владелец может снять с них наличные деньги по первому требованию.

Ликвидность отдельных компонентов денежной массы различна. Денежная масса обычно структурируется по степени ликвидности ее компонентов. По мере снижения ликвидности в состав компонентов денежной массы последовательно включаются активы, все в меньшей мере способные выполнять функцию средства платежа.

Структура денежной массы характеризуется денежными агрегатами, расположенными по мере их укрупнения (каждый предыдущий агрегат включается в последующий).

Для измерения денежной массы используются следующие денежные агрегаты: М₀, М₁, М₂, М₃.

Агрегат М₀ – это наличные деньги (бумажные и металлические) в обращении.

Агрегат М₁ включает М₀ плюс деньги на текущих счетах населения и на расчетных счетах предприятий, счетах до востребования в банках, дорожные чеки. Под деньгами в узком смысле подразумевается агрегат М₁, с помощью которого производится большинство операций обмена.

Денежный агрегат М₂ включает М₁ плюс деньги на срочных и сберегательных счетах в коммерческих банках, депозиты в специализированных финансовых учреждениях и некоторые другие активы. Денежные средства, входящие в данный агрегат, не могут непосредственно переводиться от одного лица к другому и использоваться для совершения сделок. Они выполняют главным образом функцию средства накопления. Денежный агрегат М₂ – это деньги в широком смысле слова. Он наиболее часто используется для макроэкономического анализа.

Агрегат М₃ является наиболее крупным. Он включает агрегат М₂ плюс крупные срочные депозиты, соглашения о покупке ценных бумаг с обратным выкупом по обусловленной цене, депозитные сертификаты банков, государственные (казначейские) облигации, коммерческие бумаги и др. В данный агрегат включаются государственные краткосрочные облигации (ГКО), облигации федерального займа (ОФЗ), облигации государственного сберегательного займа, облигации государственного внутреннего валютного займа.

73. Структурные средние величины, их смысл и значение

Структурные средние:

• Мода
• Медиана

Мода-величина признака, т.е. варианта, которая наиболее часто повторяется в совокупности.

Модой называется то значение признака, которая соответствует максимальной точке, теоретической кривой распределения.

Мода отражает типичный, наиболее расп распространенный вариант значения признака.
Если данные не сгруппированы, то моду определяют согласно определению.

В дискретном ряду распределения мода-варианта, кот.соответствует наибольшей частоте.
В интервальном ряду расп. сначала определяют модальный интервал(интервал содержащий моду)-ему соответствует наиб.частота.

Медиана-величина, которая делит численность упорядоченного вариационного ряда на две равные части. Одна часть имеет значение не больше, чем медиана, а другая-не меньше, чем медиана.

Для ранжированного ряда с нечетным числом членов, медианой является варианта расположенная в центре.

Для ранжированного ряда с четным числом, медиана рассчитывается, как среднеарифметическое из 2-х вариантов, расположенных в центре.

Для дискретного ряда распределения медиана рассчитывается с помощью накопленных частот. Медианой является варианта, кот.соответствует накопленная частота впервые превысившая половину общей суммы частот.
Для интервального ряда сначала, с помощью накопленных частот определяют медианный интервал, которому соответствует накопленная частота, впервые превысившая половину суммы частот.

74. Табличное представление статистических данных

В виде статистических таблиц оформляются результаты сводки и группировки материалов наблюдения.

Статистическая таблица– это особый способ краткой и наглядной записи сведений об изучаемых общественных явлениях.

Статистическая таблица имеет свое подлежащее и сказуемое. Подлежащее таблицы показывает, о каком явлении идет речь в таблице, и представляет собой группы и подгруппы, которые характеризуются рядом показателей. Сказуемым таблицыназываются числовые показатели, с помощью которых характеризуется объект, т. е. подлежащее таблицы.

Различают три вида статистических таблиц:

• простые
• групповые
• комбинационные

Простые таблицы содержат перечень отдельных единиц, входящих в состав анализируемого явления.

В групповых таблицах цифровая информация объединяется в определенные группы в соответствии с каким-либо признаком. в групповых таблицах осуществляется простая группировка показателей

Комбинированные таблицы содержат отдельные группы и подгруппы, на которые подразделяются экономические показатели, характеризующие изучаемое экономическое явление. При этом такое подразделение осуществляется не по одному, а по нескольким признакам — комбинированная группировка.

75. Условия сопоставимости абсолютных и относительных величин

76. Цепные и базисные индексы

Существуют два вида индексов (не всего, конечно, а в рассматриваемом методе): базисные и цепные.

Базисные индексы – это такие, у которых в качестве базисного значения (показателя в знаменателе) берется какой-либо фиксированный период. Последовательность базисных индексов показывает динамику показателя относительно этого периода (обычно к началу месяца, началу года). Если взять кратность периода по месяцам, то это будет февраль к январю, март к январю, апрель к январю и т.д.

Цепные индексы – в качестве базисного значения (в знаменателе) выступает предыдущий период (не фиксируется, а изменяется в зависимости от анализируемого периода). При помесячных данных это будет: февраль к январю, март к февралю, апрель к марту и т.д.

Оба вида взаимосвязаны между собой

77. Экономически активное и неактивное население

Экономически активным населением (согласно определению Международной Организации Труда) считается та часть населения в возрасте от 15 до 72 лет, которая предлагает свой труд для производства товаров и услуг.

В составе экономически активного населения выделяют категории населения, занятого экономической деятельностью, и категорию безработного населения.

К населению, занятому экономической деятельностью, относятся лица старше 16 лет, которые в рассматриваемый период:

1. выполняли работу по найму за вознаграждение, деньги или с ними расплачивались в натуральной форме;

2. временно отсутствовали на работе в связи с болезнью, отпуском, учебой и другими причинами, предусмотренными законодательством;

3. выполняли работу без оплаты на семейном предприятии.

При отнесении того или иного лица к числу занятых используется критерий одного часа, согласно которому работы в течение одного часа в отчетном периоде в сфере экономической активности достаточно, чтобы это лицо было отнесено к числу занятых.

К безработному населению относятся лица старше 16 лет, которые в рассматриваемый период:

1. не имеют работы;

2. занимаются поиском работы (самостоятельно или с помощью служб занятости);

3. готовы приступить к работе незамедлительно.

В состав безработных включаются также лица, обучающиеся по направлению служб занятости. В качестве безработных учитываются учащиеся и студенты, инвалиды и пенсионеры в том случае, если они активно занимаются поисками работы и готовы к ней приступить.

Продолжительностью безработицы считается длительность периода, в течение которого безработный ищет работу, с момента начала поиска до рассматриваемого периода (продолжительность незавершенной безработицы) или до момента трудоустройства (продолжительность завершенной безработицы).

Экономически неактивное население составляют лица в возрасте от 15 до 72 лет, которые не считаются занятыми экономической деятельностью или безработными в течение рассматриваемого периода.

Численность экономически неактивного населения может быть рассчитана как разность между численностью всего населения и численностью рабочей силы.

В составе экономически неактивного населения выделяют:

1. учащиеся и студенты, курсанты, посещающие дневные учебные заведения;

2. лица, получающие пенсию по старости и на льготных условиях, по выслуге лет;

3. лица, получающие пенсию по инвалидности;

4. лица, занятые ведением домашнего хозяйства, уходом за детьми, больными родственниками;

5. лица, получающие доход от собственности;

6. лица, отчаявшиеся найти работу, но которые готовы приступить к работе;

7. другие лица.