Градиент давления и его свойства.

Рассмотрим точку М, имеющую координаты (x, y, z) и находящуюся в жидкости(рис. 1.3). Давление в точке М – . Это давление зависит только от координат точки М. Можно записать .

На небольшом расстоянии от точки М находится точка М₁с координатами (x+dx, y+dy, z+dz).

Давление в М₁ отличается от давления р_М на некоторую величину dp: .

Давление зависит от координат точки М₁: .

Тогда .

Рис. 1.3. Градиент давления

Т.к. р является функцией координат x, y, z, то величину dp можно записать в дифференциальной форме

Вектор перемещения от точки М к точке М₁ записывается в форме

где – единичные векторы, направленные вдоль осей координат.

Определение: В физике для обозначения изменения некоторой скалярной величины G (температуры, давления) от одной точки к другой используется понятие вектора

.

(1.8)

Значит, вектор градиента давления величин

.

Можно записать в виде

.

(1.9)

Произведение двух векторов

(1.10)

или

.

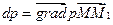Вывод: изменение давления dp является скалярным произведением двух векторов grad p и ММ₁.

Свойства вектора :

1. Если точки М и М₁ принадлежат поверхности в которой все точки испытывают одинаковые давление, то можно записать

,

тогда dp = 0.

Вывод: расположен по нормали к поверхности равного давления, проходящей через точку М.

2. Предположим, что М₁ расположена по нормали к поверхности равного давления, проходящей через точку М, тогда dp > 0. Значит скалярное произведение MМ₁ имеет положительное значение и имеет то же направление, что и ММ₁.

Вывод: направлен в сторону увеличения давления.

3. .

Вывод: величина определяется отношением разности давлений в двух точках к расстоянию между этими точками.