
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнение количества движения
В теоретической механике изучается теорема о количестве движения материальных точек, которую можно применить в гидравлике. Будем считать движение жидкости в канале (см. рис 2.37) установившемся. Распределение давления в сечениях 1-1 и 2-2 гидростатическое. В сечении 1-1 действует сила давления, направленная внутрь выделенного объема жидкости  , в сечении 2-2 – сила
, в сечении 2-2 – сила  (
(  – давление в сечениях 1-1 и 2-2,
– давление в сечениях 1-1 и 2-2,  – площади сечений). На элементарной площадке стенки канала действуют: сила реакции стенки, равная силе давления pds и сила вязкого трения τds. Проекция этих сил на ось движения равна pds sin α + τds cos α(α – угол наклона элементарной стенки какала к его оси). Суммарная проекция внешних сил, действующих на изолированную массу жидкости, равна
– площади сечений). На элементарной площадке стенки канала действуют: сила реакции стенки, равная силе давления pds и сила вязкого трения τds. Проекция этих сил на ось движения равна pds sin α + τds cos α(α – угол наклона элементарной стенки какала к его оси). Суммарная проекция внешних сил, действующих на изолированную массу жидкости, равна
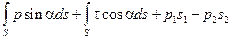 .
.

Рис. 2.37. Силы, действующие на поток жидкости в канале
Примем, что ось канала наклонена под углом θ к горизонту. Проекция веса жидкости, заключенной между выбранными сечениями равна gρVsin θ(V – объем выделенной массы жидкости).
Проекция всех сил, действующих на изолированную массу, равна
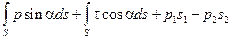 – gρVsin θ. – gρVsin θ.
| (2.40) |
Распределение скорости в контрольных сечениях может быть неравномерным. Через элементарную площадку ds контрольной поверхности в единицу времени переносится количество движения, равное  (u – местная скорость течения). Суммарное количество движения равно
(u – местная скорость течения). Суммарное количество движения равно  . Средняя скорость в контрольном сечении
. Средняя скорость в контрольном сечении  . Количество движения, подсчитанное по средней скорости равно
. Количество движения, подсчитанное по средней скорости равно 
Отношение количества движения, действительно перенесенного потоком, к количеству движения, определенного по средней скорости, называется коэффициентом Буссинеска  .
.
В единицу времени при установившемся движении изменение количества движения составит
 ,
,
где Q – расход жидкости.
Импульс действующих сил должен равняться изменению количества движения массы, на которую данный импульс действует. Следовательно, при течении жидкости в канале с учетом принятых условий соблюдается равенство
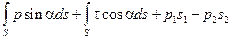 – gρVsin θ= – gρVsin θ= 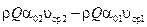 . .
| (2.41) |
Нами получено гидравлическое уравнение количества движения.
Вывод: При переходе от сечения 1-1 к сечению 2-2 проекция секундного количества движения потока изменяется на величину, равную сумме проекций всех внешних сил, действующих на объем потока, заключенный между сечениями 1-1 и 2-2.
Применяя уравнение количества движения, можно решить ряд задач гидравлики, например: теоретически определить коэффициент местного сопротивления при внезапном расширении трубы; изменение давления в трубе при равномерном отборе жидкости на одном ее участке; определение расхода газа при всасывании его через цилиндрическую трубу.
Дата добавления: 2015-04-21; просмотров: 302; Мы поможем в написании вашей работы!; Нарушение авторских прав |