
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Три формы представления уравнения Бернулли для потока реальной жидкости
Представленное выше уравнение Бернулли является уравнением Бернулли, записанное в форме удельной энергии, где:
 и
и  – удельная энергия положения в сечениях 1-1 и 2-2 потока;
– удельная энергия положения в сечениях 1-1 и 2-2 потока;
 и
и  – удельная энергия давления в этих сечениях;
– удельная энергия давления в этих сечениях;
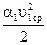 и
и  – удельная кинетическая энергия.
– удельная кинетическая энергия.
На практике при выполнении инженерных расчетов обычно применяют две другие формы представления уравнения Бернулли.
Уравнение Бернулли в форме напоров можно получить, если разделить уравнение в форме удельной энергии на g, обозначив  .
.
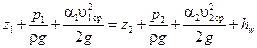 . .
| (2.50) |
Каждый член этого выражения имеет размерность длины и может быть представлен некоторой высотой (напором) (см. рис. 2.39).
Здесь  и
и  – высота положения или геометрический напор (расстояние от плоскости сравнения до центра сечения потока);
– высота положения или геометрический напор (расстояние от плоскости сравнения до центра сечения потока);
 и
и  – пьезометрическая высота или пьезометрический напор (высота поднятия жидкости в пьезометрической трубке под действием давления);
– пьезометрическая высота или пьезометрический напор (высота поднятия жидкости в пьезометрической трубке под действием давления);
 и
и  – скоростной напор (разность показаний трубки Пито и пьезометрической трубки).
– скоростной напор (разность показаний трубки Пито и пьезометрической трубки).
Сумма трех высот  и
и  – полный напор потока жидкости.
– полный напор потока жидкости.

Рис. 2.39. Опытная демонстрация уравнения Бернулли в форме напоров
Разность полных напоров двух живых сечений потока – потеря напора между этими сечениями
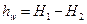 . .
| (2.51) |
С помощью уравнения Бернулли в форме напоров можно найти высотные отметки жидкостей, которые могут быть достигнуты в данной трубопроводной системе. Это уравнение широко используется при проектировании и гидравлических расчетах водопроводов.
Уравнение Бернулли в форме давлений получаем, если уравнение Бернулли в форме удельной энергии умножим на плотность ρ.

| (2.52) |
Здесь каждый член имеет размерность давления:
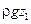 и
и  – гравитационное давление, т. е. давление, создаваемое силой тяжести;
– гравитационное давление, т. е. давление, создаваемое силой тяжести;
 и
и  – статическое давление;
– статическое давление;
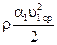 и
и  – динамическое давление;
– динамическое давление;
 – потери давления на преодоление сил трения и местные сопротивления.
– потери давления на преодоление сил трения и местные сопротивления.
Вывод:при увеличении скорости движения потока давление на этом участке падает и, наоборот – при уменьшении скорости давление увеличивается.
Уравнение Бернулли в форме давлений применяется для расчета систем вентиляции, газовых стояков внутри зданий и т.д.
Дата добавления: 2015-04-21; просмотров: 277; Мы поможем в написании вашей работы!; Нарушение авторских прав |