Сопротивление по длине при движении жидкости в цилиндрической трубе при ламинарном режиме.

При ламинарном режиме жидкость движется концентрическими слоями. Воспользуемся формулой Ньютона для напряжений трения, приняв

.

Знак «минус» указывает на то, что скорость уменьшается в направлении оси r (от центра к стенке трубы).

Составим уравнение равномерного движения жидкости для выделенного объема длиной l и радиусом r (см. рис 4.10).

Рис.4.10. Движение жидкости в прямой трубе

На выделенный объем действуют внешние силы: нормальные к живым сечениям: силы давления , и касательные силы сопротивления Т, приложенные к боковой поверхности

Уравнение равновесияэтих сил относительно направления движения:

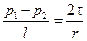или ,

или .

(4.1)

Вывод: При ламинарном движении в круглой трубе напряжение трения максимально у стенки и равно 0 на оси трубы (см. рисунок).

Закон распределения скоростей по сечению трубы можно получить из следующего уравнения

,

.

После интегрирования, получаем: .

Константу находим из граничных условий: , .

откуда ,

.

Окончательно получаем

.

(4.2)

Вывод:При ламинарном течении скорости в сечении трубки распределяются по параболическому закону (см. рис. 4.10).

Максимальная скорость на оси трубы будет при r = 0

, или .

(4.3)

Определим величину расхода жидкости через определенное сечение.

Расход элементарной струйки , где dS – площадь сечения трубки тока,

.

Полный расход

.

(4.4)

Вывод: Для того чтобы определить расход при ламинарном режиме достаточно измерить скорость на оси потока и умножить ее на половину площади живого сечения.

Определим среднюю скорость. Согласно определению .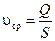

, .

Получаем

.

(4.5)

Вывод: Средняя скорость при ламинарном режиме в два раза меньше скорости на оси потока.

Коэффициент Кориолиса вычисляется из выражения .

Подставляем значения u и dS, интегрируя, получаем

.

(4.6)

Для получения закона сопротивления при ламинарном режиме вернемся к формуле расхода .

Подставим значение .

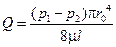, откуда .

Разделим на ρg, в результате получаем

,

где – потери давления; – потери напора.

Получаем

.

(4.7)

Вывод: Потери напора на преодоление сил сопротивления по длине при ламинарном режиме прямопропорциональны расходу и длине трубопровода и обратнопропорциональны радиусу трубы в четверной степени.