
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнение Бернулли в трех формах.
Общее уравнение энергии в интегральной форме
(Уравнение Бернулли для потока реальной жидкости)
Для двух сечений струйки невязкой жидкости это уравнение будет выглядеть следующим образом
 . .
| (2.45) |
Сумма слева представляет полную удельную энергию струйки в сечении 1-1, сумма справа – полную удельную энергию струйки в сечении 2-2. Можно записать, что
 .
.
На практике энергия струйки в начале больше энергии струйки в конце, т.к. часть энергии теряется на преодолении сил вязкости. В процессе движения вязкой жидкости запас ее механической энергии уменьшается, и на самом деле
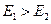 .
.
Обозначим энергию, затрачиваемую на преодоление сил сопротивления Eпот. Eпот – это та часть механической энергии, которая, вследствие вязкости, переходит в тепловую энергию. Другими словами можно сказать, что Eпот – это часть энергии, которая израсходована на преодоление гидравлических сопротивлений.
| Е1 = Е2 + Eпот. | (2.46) |
При выводе уравнения Бернулли для элементарной струйки можно было пренебречь изменением скорости и давления в пределах нормальных сечений благодаря их малым величинам. В потоке жидкости скорости и давления в пределах живых сечений различны, и это необходимо учитывать. Согласно гипотезе Ньютона, жидкость как бы прилипает к стенкам канала, по которому она течет и ее скорость равна нулю. Но с увеличением расстояния от стенки, скорость струек увеличивается. Так называемая мощность потока складывается из энергии отдельных струек
 ,
,
где N – мощность потока; dN – мощность струйки; S – площадь живого сечения потока.
Для мощности струйки можно записать:
dN = Ed  = (gz +
= (gz +  +
+  ) ρuds,
) ρuds,
где ds – площадь живого сечения струйки.
Величина удельной энергии потока равна частному от деления мощности потока на массовый расход 
 .
.
Это уравнение можно разбить на два интеграла
E =  =
= 
 ,
,
где 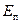 – удельная потенциальная энергия потока относительно выбранной плоскости сравнения;
– удельная потенциальная энергия потока относительно выбранной плоскости сравнения;  – удельная кинетическая энергия потока.
– удельная кинетическая энергия потока.
Для вычисления 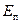 надо знать закон изменения давления по живому сечению. Для плавноизменяющихся течений ускорения и силы инерции незначительны, поэтому ими можно пренебречь. Экспериментально доказано, что в плавноизменяющемся потоке давления распределяются по закону гидростатистики gz
надо знать закон изменения давления по живому сечению. Для плавноизменяющихся течений ускорения и силы инерции незначительны, поэтому ими можно пренебречь. Экспериментально доказано, что в плавноизменяющемся потоке давления распределяются по закону гидростатистики gz  = const.
= const.
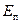 = =   gz gz  . .
| (2.47) |
Для вычисления интеграла  нужно знать закон распределения скоростей по сечению. Умножим и поделим это выражение на
нужно знать закон распределения скоростей по сечению. Умножим и поделим это выражение на  .
.

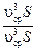 =
= 
 =
=  ,
,
где α – коэффициент, который учитывает неравномерность распределения скоростей в сечении, называется коэффициент Кориолиса. Получаем выражение для удельной кинетической энергии потока:
 = =  . .
| (2.48) |
Запишем уравнение Бернулли для двух сечений потока реальной жидкости
 . .
| (2.49) |
Полученное уравнение позволяет сделать следующие выводы:
1. При увеличении кинетической энергии потока от одного сечения к другому потенциальная энергия уменьшается, и, наоборот, с увеличением потенциальной энергии, кинетическая уменьшается.
2. Коэффициент α тем больше, чем больше скорости отдельных струек отличаются от величины средней скорости. Если скорости всех элементарных струек будут равны средней скорости, то α = 1.
Дата добавления: 2015-04-21; просмотров: 285; Мы поможем в написании вашей работы!; Нарушение авторских прав |