Характер движения жидкости в межлопастном пространстве.

Центробежный насос не обладает самовсасывающей способностью, поэтому перед началом действия их необходимо заполнять жидкостью. Они устанавливаются ниже уровня цистерны и снабжаются вакуумной ступенью или вакуумным насосом.

Когда насос заполнен, происходит следующее: жидкость из всасывающего трубопровода со скоростью 2-3 м/с поступает в подводящее устройство. Здесь с целью предотвращения закрутки потока и сохранения оси симметрии скорость жидкости увеличивается на 10-15%, затем через воронку колеса поток жидкости поступает в межлопастные каналы, где на жидкость действуют силы: тяжести, вязкости, инерции окружного движения, давления лопастей и центробежная. В результате действия указанных сил на каждую частицу жидкости её движение в каналах приобретает сложный пространственный характер (трёхмерный поток).

Основных сил две: сила давления лопастей, которая вовлекает жидкость в переносное окружное движение и сообщает жидкости окружную скорость; возникающая центробежная сила, вовлекающая жидкость в поступательное движение в направлении периферии колеса. Движение жидкости в межлопастных каналах сопровождается увеличением скорости до 1 порядка. С такой скоростью жидкость выходит в отводящее устройство. Здесь скорость жидкости преобразуется в давление, после чего поток направляется в нагнетательный трубопровод.

Когда насос работает с воздухом, происходит то же самое, но плотность воздуха меньше жидкости в 800 раз. Центробежные силы оказываются незначительными, недостаточными для создания разряжения в корпусе насоса, необходимого для всасывания. Поэтому все центробежные насосы не обладают самовсасывающей способностью, и при попадании в рабочую полость насоса воздуха, насос срывает.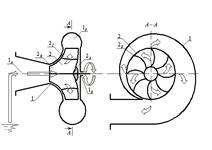

1- корпус

1_А – подводящее устройство

1_Б – отводящее устройство

1_В – камера уплотнения вала

2 – рабочее колесо

2_А – задний диск рабочего колеса

2_Б – лопасть (лопатка) рабочего колеса

2_В – воронка

2_Г – передний диск рабочего колеса

Выражение для напора получено при условии что , а так же когда, через межлопастные каналы рабочего колеса движется идеальная невязкая жидкость. При движении вязкой жидкости и конечном числе лопастей картина движения жидкости будет иной по двум причинам:

–потому что при конечном числе лопастей траектории частиц находятся на удалении от лопастей будут иметь траектории, отличающиеся от профиля лопастей

–при конечном числе лопастей в межлопастных каналах под действием сил инерции окружного движения возникнет циркуляционное движение жидкости, противоположное направлению вращения колеса.

Различают 3 вида потерь: трение, входа и выхода жидкости, вихреобразования.

1. Потери трения – следствие трения между слоями жидкости, между стенками насоса и жидкостью.

2. Потери входа и выхода – изменение величины и направления скорости.

3. Потери вихреобразования – следствие отрыва жидкости от лопастей в зонах пониженного давления.

Гидравлические потери снижают энергию потока и уменьшают КПД насоса. Гидравлические потери учитывают введением КПД:

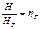, где – гидравлический КПД насоса;

Для центробежных насосов .

Величина гидравлических потерь зависит от степени гидродинамического совершенства формы межлопастных каналов рабочего колеса и формы отвода и, второе, от степени шероховатости стенок. Гидравлический КПД насоса учитывает не только потери в межлопастных каналах, но также потери в отводящем устройстве, так как выделить и измерить эти потери в отдельности невозможно.

Предпочтительно пользоваться характеристиками, полученными экспериментальным путем.

Отличающийся высокой сложностью процесс движения жидкости в каналах колёс центробежного насоса не имеет точного масштабного описания, которое позволило бы только расчетным путём находить оптимальные геометрические параметры рабочих колёс. Данные для уточнения расчётов получают опытным путём в результате испытания моделей насосов, создаваемых для этой цели. Такой путь создания центробежных насосов не является единственным. Это объясняется тем, что расчёт центробежных насосов производится с испытанием законов подобия. Это позволяет подобрать модель с высокими параметрами из числа существующих насосов и пересчитать размеры насоса на условия работы с использованием уравнений подобия.

Подобие предполагает:

1. Геометрическое подобие проточных частей;

2. Кинематическое и динамическое подобия потоков жидкости.

Геометрическое подобие предполагает постоянство пропорциональности любых соответствующих линейных размеров и углов проточных частей рабочих колёс. Для линейных размеров это условие выражается отношением:

, где:

– линейный размер натурального насоса,

– линейный размер модели.

Кинематическое подобие предполагает постоянство пропорциональностей скоростей жидкости:

.

Для переносных окружных скоростей это условие выражается отношением:

.

Динамические подобия предполагают постоянство пропорциональностей сил, действующих на жидкость в любых соответствующих точках потока. Принимая во внимание условия подобия и используя выражения для подачи, получаем:

;

, при ;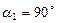

.

Решая их, получаем основные уравнения подобия колёс центробежных насосов.

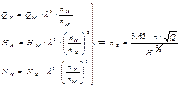
где – коэффициент быстроходности.

Если насос при напоре создаёт подачу , то .

Все центробежные насосы с одинаковой величиной являются подобными.

Подача насоса простого действия отличается неравномерностью.

Неравномерность оценивается величиной отношения:

,

где:

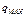– максимальная секундная подача насоса,

– средняя подача.

Степень неравномерности подачи зависит от кратности действия.

Движение жидкости в межлопастных каналах сопровождается приращением её скорости на величину до 1-го порядка. Для повышения давления жидкости её скорость необходимо понизить. Понижение ск4орости в ространстве за колесом осуществляется с помощью отводящего устройства. Для пояснения этого процесса рассмотрим движение жидкости в свободном пространстве за колесом. При этом допускают, что жидкость идеальная невязкая, и её движение за колесом струйное, осесимметричное. В пространстве за колесом, лопасти на жидкость не действуют, поэтому её частицы будут иметь только окружную скорость , радиальную и абсолютную . В частности, на окружности входа жидкости в пространство за колесом , на окружности произвольного радиуса .

– угол скорости жидкости,

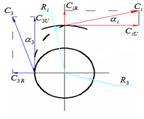
– угол скорости на ,

Для анализа изменения скорости жидкости используется выражение для моментов количества движения. Аналогично для анализа окружной составляющей движения используется закон сохранения моментов количества движения.

где, 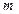– масса жидкости.

Идеальная жидкость перемещается с на 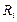без потерь энергии и без изменения момента количества движения.

. ,

где – момент количества движения;

Для исследования изменения радиальной составляющей скорости используется закон сохранения массы.

Закон сохранения массы предполагает постоянство расхода жидкости в любом сечении потока:

Изменяется абсолютная скорость, т.е. она уменьшается прямо пропорционально удалению жидкости от оси вращения колеса. Устройство должно иметь форму, обеспечивающую удаление жидкости от оси вращения колеса.