ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

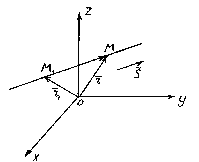Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки М₁ и вектора 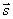, параллельного этой прямой.

Вектор 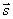, параллельный прямой, называется направляющим вектором этой прямой.

Итак, пусть прямая l проходит через точку М₁(x₁, y₁, z₁), лежащую на прямой параллельно вектору .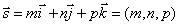

Рассмотрим произвольную точку М(x,y,z) на прямой. Из рисунка видно, что .

Векторы 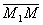и 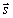коллинеарны, поэтому найдётся такое число t, что 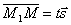, где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М₁ и М соответственно через 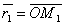и , получаем 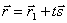. Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки М, лежащей на прямой.

Запишем это уравнение в координатной форме. Заметим, что 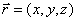, и 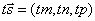отсюда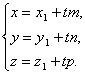

Полученные уравнения называются параметрическими уравнениями прямой.

При изменении параметра t изменяются координаты x, y и z и точка М перемещается по прямой.