Уравнение прямой с угловым коэффициентом. Пусть дана прямая L на координатной плоскости Оху.

Пусть дана прямая L на координатной плоскости Оху.

Определение. Углом наклона прямой к оси абсцисс называется уголповорота оси абсцисс вокруг любой ее точки против часовой стрелки до положения параллельности (или совпадения) с данной прямой.

рис.1.

Из определения следует, что угол наклона прямой L к оси Ох может изменяться от нуля до : . Если прямая , то .

Пусть

(1)

– общее уравнение прямой L, где – нормальный вектор прямой L и . Тогда и (см. рис.1). Выразим у изуравнения (1)

.

, .

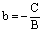Уравнение прямой L принимает вид:

.

Определение. Уравнение прямой вида

(2)

называется уравнением прямой с угловым коэффициентом, а коэффициент k называется угловым коэффициентом данной прямой.

Теорема. В уравнении прямой с угловым коэффициентом

угловой коэффициент k равен тангенсу угла наклона прямой к оси абсцисс:

. (3)

Доказательство. 1) Если прямая , то и . С другой стороны, ее нормальный вектор и .

Тогда и, следовательно, , ч.т.д.

2) Пусть , тогда , и . Пусть F – точка пересечения прямой L с осью абсцисс. Тогда

, .

Опишем окружность единичного радиуса с центром в точке F , а в точке оси Ох с координатой проведем касательную m к этой окружности. См. рис.2.

рис.2.

Выберем положительное направление на прямой m, так, чтобы . Тогда ось m является осью тангенсов для данной единичной (тригонометрической) окружности.

Пусть Р – точка пересечения прямой L с осью тангенсов m. Тогда, с одной стороны, , где – угол наклона прямой L к оси Ох, а, с другой стороны, точка и , откуда и следует равенство , ч.т.д.

Теорема доказана.

Заметим, что приведенное доказательство принадлежит автору этих лекций. Достоинством этого доказательства является то, что оно не зависит ни от величины угла наклона , ни от величины коэффициента .

В заключение отметим, что коэффициент b в уравнении (2) равен величине отрезка, отсекаемого прямой от оси ординат (см. рис.2).

Линию на плоскости можно задать при помощи двух уравнений:

(4)

где х и у — координаты произвольной точки М(х;у), лежащей на данной линии, a t — переменная, называемая параметром; параметр t определяет положение точки (х; у) на плоскости.

Например, если x=t+l, y=t²,тo значению параметра t = 2 соот­ветствует на плоскости точка (3; 4), т. к. х = 2 + 1 = 3, у = 2² = 4.

Если параметр t изменяется, то точка на плоскости перемещается, описывая данную линию. Такой способ задания линии называется пара­метрическим, а уравнения (4) - параметрическими уравнениями ли­нии.

Далее, положение прямой L на плоскости вполне определяется заданием какой-либо ее точки М(х₁,у₁) и вектора S=mi+nj , параллельного L или лежащего на ней. Этот вектор называетсянаправляющим вектором прямой L.

Пусть М(х,у) - произвольная точка прямой L. Так как векторы

коллинеарны (по условию), то их координаты пропорциональны.

Это уравнение называется каноническим уравнением прямой.

Канонические уравнения прямой, проходящей через точку М0 (х0у0z0) и имеющей направляющий вектор В чем смысл этого уравнения? На прямой известна фиксированная точка Н0 (х0, у0, z0). Рассмотрим на этой прямой еще текущую точку М (х, у, z). Вектор есть направляющий вектор нашей прямой, то есть он коллинеарен любому вектору, лежащему на ней, в том числе и вектору . То есть, вектора и коллинеарны, а коллинеарность векторов означает пропорциональность координат и является уравнением прямой. Рассмотрим пример: Даны вершины пирамиды А1(1,2,3) А2(3,5,4) А3(1,5,2) А4(3,4,8) Найти: 1) Длину ребра А1А2. Длина ребра есть длина вектора A1A2 =(3-1, 5-2, 4-3) = (2,3,1) 2) Угол между ребрами А1А2 и А1А4. Угол между ребрами есть угол между векторами A1A2и А1А4 А1А2=(2,3,1) А1А4=(2,2,5) 3) Угол между ребром А1А4 и гранью А1А2А3.

Поскольку угол между прямой и плоскостью есть угол между прямой и ее проекцией на плоскость, мы можем рассмотреть угол, дополняющий  до  /2 . Это угол между нормалью к плоскости и А1А4. В качестве нормали возьмем векторное произведение A1A2(2,3,1)и A1A3(0,3,-1)

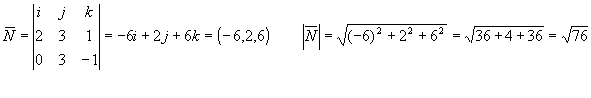
4) Площадь грани А1А2А3. SА1А2А3 есть площадь треугольника А1А2А3 и половина площади параллелограмма, построенного на А1А2и А1А3 , которая равна длине вектора N, вычисленного выше. Найдем объем пирамиды А1 А2 А3 А4. 5) Чтобы найти объем пирамиды, мы можем воспользоваться выражением через объем призмы который, как мы знаем, равен смешанному произведению векторов, на которых, как на ребрах построена призма. 6) Уравнения прямой А1А2: Направляющий вектор - А1А2 , точка, через которую проходит прямая – А1. Используем уравнение прямой, проходящей через данную точку в заданном направлении (то есть имеющей данный направляющий вектор) 7) Уравнение плоскости А1А2А3: опорные точки – А1,А2,А3 Воспользуемся уравнением плоскости, проходящей через три точки: разложим по элементам 1-го столбца: (х - 1)(-6) - 2[(у - 2)(-1) - 3(z - 3)] = 0 6(1 - х) - 2(2 - у - 3z + 9) = 0 6 - 6х - 22 + 2у + 6z = 0 6х - 2у - 6z + 16 = 0 или 3х - у - 3z + 8 = 0 8) Известно, что наша прямая проходит через точку А4 (3,4.8). Используем уравнение прямой, проходящей через заданную точку в заданном направлении (с заданным направляющим вектором).

Определение. Если заданы две прямые y = k₁x + b₁, y = k₂x + b₂, то острый угол между этими прямыми будет определяться как

.

Две прямые параллельны, если k₁ = k₂.

Две прямые перпендикулярны, если k₁ = -1/k₂.

Теорема. Прямые Ах + Ву + С = 0 и А₁х + В₁у + С₁ = 0 параллельны, когда пропорциональны коэффициенты А₁ = lА, В₁ = lВ. Если еще и С₁ = lС, то прямые совпадают.

Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых.