Векторов. Примеры линейно зависимых и независимых векторов.

Определение. Вектором называется направленный отрезок (упорядоченная пара точек). К векторам относится также и нулевой вектор, начало и конец которого совпадают.

Определение. Длиной (модулем) вектора называется расстояние между началом и концом вектора.

Определение. Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.

Определение. Векторы называются компланарными, если существует плоскость, которой они параллельны.

Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.

Определение. Векторы называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые модули.

Всякие векторы можно привести к общему началу, т.е. построить векторы, соответственно равные данным и имеющие общее начало. Из определения равенства векторов следует, что любой вектор имеет бесконечно много векторов, равных ему.

Определение. Линейными операциями над векторами называется сложение и умножение на число.

Суммой векторов является вектор -

Произведение - , при этом коллинеарен .

Вектор сонаправлен с вектором ( ­­ ), если a > 0.

Вектор противоположно направлен с вектором ( ­¯ ), если a < 0.

Линейная зависимость векторов.

Определение. Векторы называются линейно зависимыми, если существует такая линейная комбинация , при не равных нулю одновременно a_i , т.е. .

Если же только при a_i = 0 выполняется , то векторы называются линейно независимыми.

Свойство 1. Если среди векторов есть нулевой вектор, то эти векторы линейно зависимы.

Свойство 2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.

Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.

Свойство 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны.

Свойство 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.

Свойство 6. Любые 4 вектора линейно зависимы.

1. Покажем, что A={ 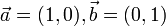}-линейнонезависимая система.

Решение: α(1,0)+β(0,1)=(0,0) ↔ (α,0)+(0,β)=(0,0) ↔ α=0, β=0, следовательно, A линейно-независимая система.

1. Покажем, что A={ 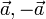} - линейно-зависимая система.

Решение. Найдём нетривиальную комбинацию, равную .

, т.е.