Проекция вектора на ось, свойства проекций. Направляющие косинусы.

Рассмотрим в пространстве прямоугольную систему координат OXYZ. Выделим на координатных осях ОХ, ОY и OZ единичный вектор (орт) И обозначим их i, j, k.

M₃

M

a

k

j M₂

i 0

M₁ N

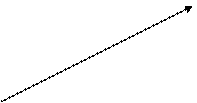
Выберем произвольный вектор а и совместим его начало с начало координат а = │ОМ│. Найдем проекции вектора а на координатные оси. Проведем через конец вектора ОМ плоскости параллельно координатным плоскостям. Точки пересечения этих плоскостей с осями координат обозначим соответственно М₁, М₂, М₃., получим прямоугольный параллепипед , одной из диагоналей которого является вектор ОМ. Тогда: пр_ха = │ОМ₁│, пр_y│ОМ ₂│, пр_z│ОМ₃│. По определению суммы нескольких векторов находим: a = OM₁ + М₁N + NM. Т.к. М₁N = OM₂; NM = OM₃, то

а = OM₁ + OM₂ + OM₃ (1)

Но OM₁ = │OM₁│i; OM₂ = │OM₂│j; OM₃ = │OM₃│k (2)

Обозначи м проекцию а = ОМ, на оси ОХ, ОY и ОZ, соответственно а_х, а_y и а_z, то есть OM₁ = а_х ; OM₂ = а_y ; OM₃ = а_z. Из равенства (1) и (2) получаем:

а = а_хi + а_yj + а_zk (3)

Эта формула является основной в векторном исчислении и называется разложением вектора по ортам координатных осей. Числа а_х, а_y и а_z называются координатами вектора а, то есть координаты вектора - есть его проекции на соответствующие координатные оси.

Векторное равенство (3) часто записывают в символическом виде: а (а_х; а_y; а_z)_. Равенство b (b_х; b_y; b_z) означает что b = b_хi + b_yj + b_zk. Зная проекции вектора а, можно легко найти выражение для модуля вектора. На основании о длине диагонали прямоугольного парралелепипеда: │ОМ│² = │OM₁│² + │OM₂│² + │OM₃│². Отсюда имеем:

(4)

Пусть углы вектора а с осями ОХ, OY и OZ ,соответственно, равны α, β и γ. По свойству проекций вектора на ось имеем:

Следовательно:

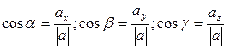(5)

Числа cosα, cosβ и cosγ называются направляющими косинусами вектора а. Подставим выражение (5) в равенство (4):

сosα² + cosβ² + cosγ² = 1

То есть сумма квадратов направляющих косинусов нулевого вектора равна 1. Легко заметить, что координатами единичного вектора е (cosα; cosβ; cosγ)

Итак, задав координаты вектора, всегда можно определить его модуль и направление (то есть сам вектор).

Действия над векторами, заданными проекциями.

Пусть векторы а = (а_х; а_y; а_z) и b = (b_х; b_y; b_z) заданы своими проекциями на оси координат OX, OY и OZ или что тоже самое:

а = а_хi + а_yj + а_zk

b = b_хi + b_yj + b_zk

1. Проеция вектора 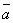на ось l равна произведению модуля вектора 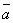на косинус угла между вектором и осью:

Доказательство. Ясно, что проекция вектора не изменится при его параллельном переносе, поэтому достаточно рассмотреть случай, когда начало вектора совпадает с началом отсчёта O оси l. Так как координата проекции начала равна нулю, то обозначим .

1. Если угол φ острый, то из прямоугольного получаем . Откуда или

2. Если угол φ тупой, то x< 0, . Тогда из 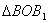или 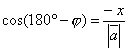. Т.е. .

2. Проекция суммы двух векторов на ось равна сумме проекций векторов на ту же ось: .

Доказательство. Пусть . Обозначим через x₁, x₂ и x₃ координаты проекций A₁, B₁, C₁ на ось l точек A, B и C. Тогда 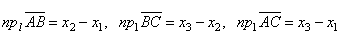. Но .

Это свойство можно обобщить на случай любого числа слагаемых.

3. Если вектор 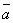умножается на число λ, то его проекция на ось также умножается на это число:

.

Доказательство. Пусть угол между вектором 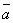и осью .

Если λ > 0, то вектор имеет то же направление, что и 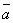, и составляет с осью такой же угол .

При λ > 0 .

Если же λ < 0, то и 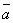имеют противоположные направления и вектор составляет с осью угол π – φ и .

Следствие. Проекция разности двух векторов на ось равна разности проекций этих векторов на ту же ось.