Примеры. 1. Написать уравнение плоскости, проходящей через точку М1(2;-3;4) параллельно прямым и .

1. Написать уравнение плоскости, проходящей через точку М₁(2;-3;4) параллельно прямым и .

Так как M₁ α, то уравнение плоскости будем искать в виде

.

Применяя условие параллельности прямой и плоскости, получим систему линейных уравнений

Отсюда

Итак, или .

2. Найти угол между прямой и плоскостью .

Направляющий вектор прямой . Нормальный вектор плоскости . Следовательно,

3. Найдите точку, симметричную данной М(0;-3;-2) относительно прямой .

Составим уравнение плоскости α перпендикулярной l. M α, . Следовательно, или .

Найдём точку пересечения прямой l и α:

Итак, N(0.5;-0.5;0.5). Пусть искомая точка М₁ имеет координаты М₁(x,y,z). Тогда очевидно равенство векторов 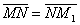, т.е. (0,5;2,5;2,5)=(х-0.5;у+0.5;z-0.5). Откуда x=1, y=2,z=3 или М₁(1;2;3)..

5. Кривые второго порядка: окружность, эллипс, гипербола, парабола,

Их канонические уравнения эксцентриситет, директрисы, асимптоты