Прямоугольные координаты точки на плоскости

Положение точки на плоскости проще всего определить при помощи прямоугольной системы координат (декартовы координаты), которую мы определим следующим образом:

1) выберем две взаимно перпендикулярные прямые - две оси координат (ось абсцисс и ось ординат), точка их пересечения называется начало координат (обозначим буквой O);

2) на каждой оси выберем положительное направление;

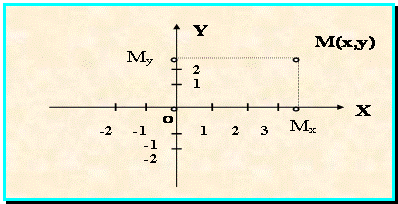Рис. 1.1.

3) для каждой оси выберем единицу длины.

Положение точки М относительно выбранной системы координат определяется двумя координатами - абсциссой х (число, равное длине oм_х) и ординатой у (длина oм_у). Эти два числа полностью определяют положение точки на плоскости.

Отрезок, соединяющий начало координат с точкой М, называется ее радиусом-вектором.

Рис. 1.2.

Обозначим через j угол, образованный ОМ с положительным направлением оси Ох, и через r - его длину, тогда можно координаты точки определить следующим образом:

(1.1)

При решении различного рода задач, иногда выгодно, вместо данной системы координат Оху, решать задачу в другой системе координат и тогда возникает вопрос о переходе от одной системы координат к другой и обратно. Другими словами, выбирается система координат О'х'у', определенным образом ориентированная относительно первой Оху.

Рассмотрим простейший случай, когда происходит простой параллельный перенос системы координат. Определение. Параллельным переносом осей координат называют переход от системы координат Оxy к новой системеО₁x₁y₁, при котором меняется положение начала координат, а направление осей и масштаб остаются неизменными.

Пусть начало новой системы координат О'х'у', по отношению к старой имеет координаты О'(а,b). Возьмем произвольную точку М(х,у) в старой системе координат, которая в новой системе будет иметь некоторые «новые координаты» (х'у') (См. рис.1.2.1).

Тогда получаем, что

х' = х – а,

у' = у – b

(1.1.1)

т.е. новые координаты точки М(х'у') равны ее старым координатам минус координаты нового начала.