Предел суммы, произведения и частного функции.

Теорема 2.

Теорема 3.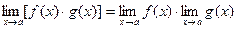

Теорема 4. при

Доказательство теоремы 2. Представим f(x) = A + a(x), g(x) = B + b(x), где

, тогда

f(x) ± g(x) = (A + B) + a(x) + b(x)

A + B = const, a(х) + b(х) – бесконечно малая, значит

Теорема доказана.

Доказательство теоремы 3. Представим f(x) = A + a(x), g(x) = B + b(x), где

, тогда

A×B = const, a(х) и b(х) – бесконечно малые, значит

Теорема доказана.

Доказательство:

Из теоремы о связи между пределом и бесконечно малой величиной следует:

;

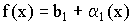Получаем:

7. Первый замечательный предел.

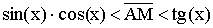
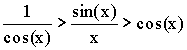
Так как , то .

Следствия из теоремы:

1)

2)

3)

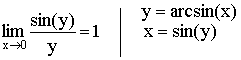
4)

5)

8.Второй замечательный предел. Число "е".

Доказательство:

Бином Ньютона:

, где .

Используем бином Ньютона для доказательства неравенства:

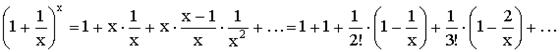
Отсюда заключаем, что , а значит .

Следствия из теоремы:

1)

2)

3)

4)

Число е.

Рассмотрим последовательность {x_n} = .

Если последовательность {x_n} монотонная и ограниченная, то она имеет конечный предел.

По формуле бинома Ньютона:

или, что то же самое

Покажем, что последовательность {x_n} – возрастающая. Действительно, запишем выражение x_n+1 и сравним его с выражением x_n:

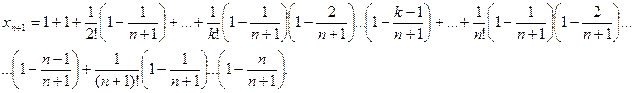Каждое слагаемое в выражении x_n+1 больше соответствующего значения x_n, и, кроме того, у x_n+1 добавляется еще одно положительное слагаемое. Таким образом, последовательность {x_n} возрастающая.

Докажем теперь, что при любом n ее члены не превосходят трех: x_n < 3.

Итак, последовательность - монотонно возрастающая и ограниченная сверху, т.е. имеет конечный предел. Этот предел принято обозначать буквой е.

Из неравенства 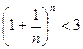следует, что е £ 3. Отбрасывая в равенстве для {x_n} все члены, начиная с четвертого, имеем:

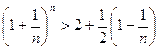
переходя к пределу, получаем

Таким образом, число е заключено между числами 2,5 и 3. Если взять большее количество членов ряда, то можно получить более точную оценку значения числа е.

Можно показать, что число е иррациональное и его значение равно 2,71828…

Аналогично можно показать, что , расширив требования к х до любого действительного числа:

Предположим:

Найдем

Число е является основанием натурального логарифма.

Выше представлен график функции y = lnx.