
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение положения центра тяжести однородных плоских фигур.
Статический момент площади сечения. Применение в расчетах.
Статическим моментом плоского сечения относительно некоторой оси называется, взятая по всей его площади А, сумма произведений площадей элементарных площадок dA на их расстояния от этой оси (рис.):

 (3)
(3)

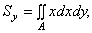 (4)
(4)
 (5)
(5)
где yc – расстояние от центра тяжести всего плоского сечения до оси x; xc – расстояние от центра тяжести всего сечения до оси y.
Статический момент сложного сечения относительно некоторой оси равен сумме статических моментов всех частей этого сечения относительно той же оси:

 (6)
(6)
В формулах (6) введены обозначения: А1, А2, …, Аn – площади простых элементов, составляющих плоское сложное сечение; x1, y1, x2, y2, x3, y3, … , xn, yn – координаты центров тяжести простых составляющих сложного плоского сечения относительно выбранных осей х и у.
Определение положения центра тяжести однородных плоских фигур.
Из выражений (4) можно определить координаты центра тяжести плоского сечения:
 (7)
(7)
Для сложного поперечного сечения формулы (7) можно представить в следующем виде
 (8)
(8)
Зависимости между статическими моментами одного и того же сечения относительно двух параллельных друг другу осей х и х1, а также у и у1 имеют вид:
 (9)
(9)
где параметры a, b показаны на следующем рисунке:

Указания:
1. Изменение положительного направления оси у вызывает изменение знака статического момента Sx. Аналогично, изменение положительного направления оси х вызывает изменение знака статического момента Sy.
2. Статический момент сечения равен нулю относительно любой оси, проходящей через центр тяжести этого сечения.
3. Если плоское сечение имеет ось симметрии, то эта ось всегда проходит через центр тяжести плоского сечения, а поэтому, согласно п.2, статический момент сечения относительно оси симметрии всегда равен нулю.
4. Если плоское сечение имеет две оси симметрии, то центр тяжести сечения лежит на пересечении этих осей симметрии.
Дата добавления: 2015-04-21; просмотров: 239; Мы поможем в написании вашей работы!; Нарушение авторских прав |