Моменты инерции простых сечений

Вычислим моменты инерции простейших фигур.

Прямоугольник

Определим моменты инерции относительно осей, совпадающих со сторонами, и относительно центральных осей.

По определению .

Рис. 4.8

Элемент площади равен dA = bdy,

следовательно .

По формуле , откуда, учитывая что А = bh, y_c = 0,5h, находим

.

Аналогично получим и .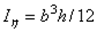

Треугольник

Момент инерции относительно оси х, cовпадающей с основанием,

.

Но dA = b(y)dy, b(y) = (b/h)(h-y).

Cледовательно,

.

Рис. 4.9

По формуле параллельного переноса , откуда .

Круг

Для любых центральных осей 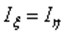, поэтому .

Как известно, полярный момент инерции круга равен .

Рис. 4.10

Следовательно, .

Кольцо ( ).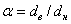

Момент инерции относительно оси (рис.4.11) можно определить как разность моментов инерции наружного и внутреннего круга:

.

Для тонкого кольца существует приближенная формула , где d_ср – средний диаметр, t - толщина кольца.