Главные оси и главные моменты инерции

Рассмотрим, как изменяются моменты инерции плоского сече­ния при повороте осей координат из положения x и y к положению u и v. Из рис.

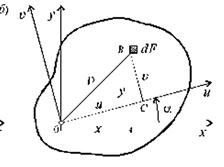
легко установить, что

u = y sin a + x cos a; v = y cos a - x sin a . (3.10)

Из выражений:

с учетом (3.10) после несложных преобразований получим:

(3.11)

Складывая первые два уравнения, получим:

I_u + I_v = I_x + I_y = I_r , (3.12)

где ; I_r - полярный момент инерции сечения, величи­на которого, как видно, не зависит от угла поворота координатных осей.

Дифференцируя в (3.11) выражение I_u по a и приравнивая его нулю, находим значение a = a₀ , при котором функция I_u прини­мает экстремальное значение:

. (3.13)

С учетом (3.12) можно утверждать, что при a = a₀ один из осе­вых моментов I_u илиI_v будет наибольшим, а другой наименьшим. Одновременно при a = a₀ I_uvобращается в нуль, что легко установить из третьей формулы (3.11).

Декартовы оси координат, относительно которых осевые мо­менты инерции принимают экстремальные значения, называются главными осями инерции.Осевые моменты инерции относи­тельно главных осей называются главными и определяются из (3.11) с учетом (3.13) и имеют вид:

. (3.14)