Байесово решающее правило классификации (в распознавании образов) при непрерывных признаках.

Билет 1

Считаем, что имеются m классов и один или несколько признаков X.Сами признаки и их связь с классами являются статистическими.

Обозначим через условные плотности распределения вероятности для признаков (если истинным является i-йкласс), а через P(i), i=1,2, - априорные вероятности для классов. Найдем по формуле Байеса апостериорные вероятности классов при условии измерения признаков x:

При распознавании выносим решение о том классе, для которого апостериорная вероятность больше.

Решающее правило:

Принимается решение об j-м классе, если

Преобразуем к эквивалентному виду: принимается решение о j-м классе, если

Вероятность ошибки классификации при m = 2:

Недостатком этих критериев является то, что в них не присутствует информация о предпочтениях одних классов перед другими. Если единичные веса заменить произвольными, то получим общую форму записи среднего риска, и решающее правило будет находиться из критерия его минимума:

получаем правило классификации:

принимается решение об j-м классе, если выполняется (m-1) неравенств:

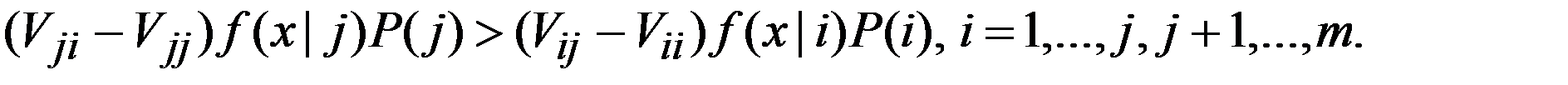
Если условные плотности распределения вероятности классов P(j) неизвестны, то их можно заменить оценками (параметрическими или непараметрическими), построенными по обучающей выборке.