
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Прямой метод восстановления решающей функции (при классификации в распознавании образов).
Имеется обучающая выборка:  , когда истинным является первый класс;
, когда истинным является первый класс;  , когда истинным является второй класс; общего объёма
, когда истинным является второй класс; общего объёма  . Вводится фиктивная переменная y, указывающая на принадлежность к тому или иному классу каждого выборочного значения обучающей выборки: например, для двух классов:
. Вводится фиктивная переменная y, указывающая на принадлежность к тому или иному классу каждого выборочного значения обучающей выборки: например, для двух классов:
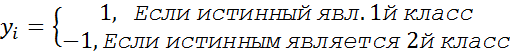
Задаётся уравнение решающей функции с точностью до параметров  , например,
, например,  , где
, где  - известные базисные функции, и из некоторого критерия, например из критерия наименьших квадратов
- известные базисные функции, и из некоторого критерия, например из критерия наименьших квадратов
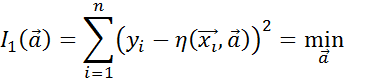
вычисляются параметры  решающей функции.
решающей функции.
Основной проблемой при данном подходе является выбор базисных (опорных) функций  . Для каждой группы объектов классификации и выборных классов существуют свои наборы базисных функций. Кроме критерия наименьших квадратов используются другие критерии, например, знаковый критерий:
. Для каждой группы объектов классификации и выборных классов существуют свои наборы базисных функций. Кроме критерия наименьших квадратов используются другие критерии, например, знаковый критерий:
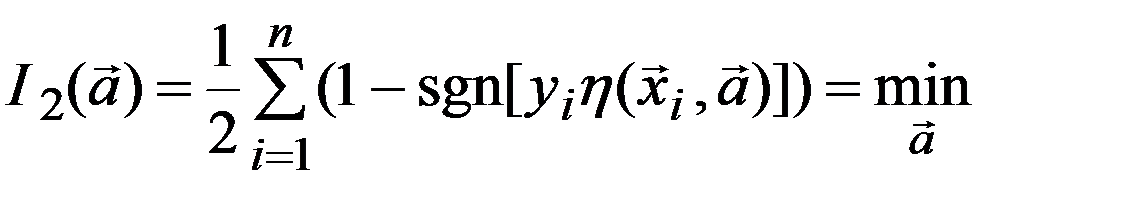
Здесь sgn[.] – знаковая функция. Она равна 1 при положительном значении аргумента (при этом осуществляется правильная классификация с помощью решающей функции  : знаки у y и
: знаки у y и  совпадают) и равна -1 при отрицательном значении аргумента (при этом происходит неправильная классификация на основе решающей функции
совпадают) и равна -1 при отрицательном значении аргумента (при этом происходит неправильная классификация на основе решающей функции  ). При правильной классификации на всех точках обучающей выборки показатель I2 равен нулю. Чем на большем числе точек осуществляется неправильная классификация, тем большее значение принимает I2. Экстремальная функция в зависимости от параметров
). При правильной классификации на всех точках обучающей выборки показатель I2 равен нулю. Чем на большем числе точек осуществляется неправильная классификация, тем большее значение принимает I2. Экстремальная функция в зависимости от параметров  является кусочно-постоянной. Из-за этого при поиске её минимума неприменимы алгоритмы дифференцируемой оптимизации. С целью устранения этого недостатка вводятся более гладкие показатели качества классификации, например:
является кусочно-постоянной. Из-за этого при поиске её минимума неприменимы алгоритмы дифференцируемой оптимизации. С целью устранения этого недостатка вводятся более гладкие показатели качества классификации, например:
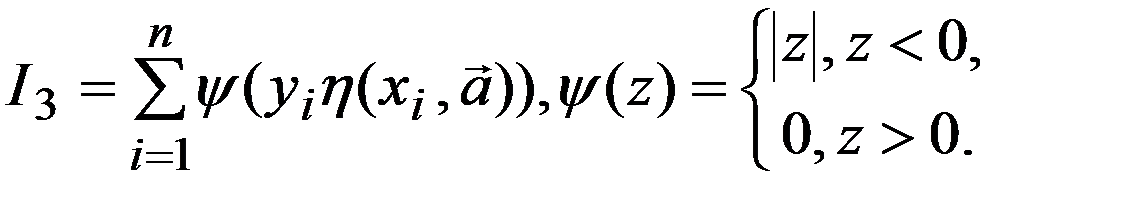
Дата добавления: 2015-04-18; просмотров: 281; Мы поможем в написании вашей работы!; Нарушение авторских прав |