Персептроны.

Имеется обучающая выборка: , когда истинным является первый класс; , когда истинным является второй класс; общего объёма . Вводится фиктивная переменная y, указывающая на принадлежность к тому или иному классу каждого выборочного значения обучающей выборки: например, для двух классов:

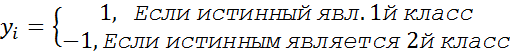
Задаётся уравнение решающей функции с точностью до параметров , например, , где - известные базисные функции.

Далее остается только найти параметры решающей функции. Это можно сделать, например, с помощью знакового критерия:

Здесь sgn[^.] – знаковая функция. Она равна 1 при положительном значении аргумента (при этом осуществляется правильная классификация с помощью решающей функции : знаки у y и 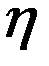совпадают) и равна -1 при отрицательном значении аргумента (при этом происходит неправильная классификация на основе решающей функции ).

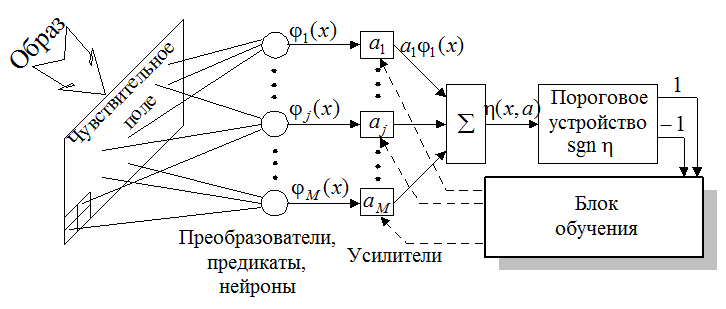Задача параллельного вычислительного устройства персептронного типа, приведенного на рисунке, заключается в разрешении приведенного знакового критерия путем вычисления блоком обучения вектора искомых параметров .

2. Сортировка последовательностей: простое слияние, естественное слияние.

Простое слияние. Наиболее простым и в то же время основополагающим методом сортировки данных на основе слияния является сортировка простым слиянием. Она выполняется следующим образом:

1. Последовательность а разбивается на две половины: b и с. Разбиение происходит следующим образом: первый элемент последовательности a записывается в последовательность b, второй элемент последовательности a записывается в последовательность c, третий – снова в b, четвертый – в c и т. д.

2. Обе последовательности b и с сливаются в a. При этом одиночные элементы последовательностей b и с сравниваются и сливаются в последовательность a в порядке возрастания (убывания), образуя упорядоченные пары.

3. Полученная последовательность а вновь разбивается на две – b и c. Данный шаг аналогичен шагу 1, однако разбиение происходит не на единичные элементы, а на упорядоченные пары. То есть первая пара последовательности a записывается в последовательность b, вторая – в последовательность c, третья пара последовательности a записывается в последовательность b, четвертая – в c и т. д.

4. Слияние последовательностей b и с в последовательность a. При этом поочередно сравниваются элементы соответствующих пар последовательностей b и с и сливаются в последовательность a в порядке возрастания (убывания), образуя упорядоченные четверки.

5. Повторяя предыдущие шаги, разбиваем и сливаем четверки в восьмерки и т. д., каждый раз удваивая длину слитых подпоследовательностей до тех пор, пока не будет упорядочена целиком вся последовательность а.

В качестве примера рассмотрим последовательность

44 55 12 42 94 18 06 67

На первом шаге разбиение дает последовательности

44 12 94 06

55 42 18 67

Слияние отдельных компонент (которые являются упорядоченными последовательностями длины 1) в упорядоченные пары дает

44 55 ' 12 42 ' 18 94 ' 06 67

Новое разбиение пополам и слияние упорядоченных пар дают

12 42 44 55 ' 06 18 67 94

Третье разбиение и слияние приводят, наконец, к нужному результату.

06 12 18 42 44 55 67 94.

Естественное слияние. Алгоритм работает по принципу простого слияния и отличается от него лишь способом разбиения исходной последовательности на блоки (секции). В естественном слиянии на каждом шаге алгоритма последовательность разбивается на группы УЖЕ ОТСОРТИРОВАННЫХ элементов, например последовательность 30, 12 13 1 2 3 будет разбита так: 30 ‘ 12 13 ‘ 1 2 3. Далее выполняются операции разбиения исходной последовательности a на подпоследовательности b и c, и их слияние, аналогично сортировке прямым слиянием.

Вычислительная сложность в сортировке ЕС в худшем случае оценивается аналогично прямому слиянию, но дает заметно лучший результат.