
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Билет 7. Ортогональные планы 1 порядка при построении линейной статистической модели объекта.
Ортогональные планы 1 порядка при построении линейной статистической модели объекта.
 Считаем, что входами объекта являются
Считаем, что входами объекта являются  , а выходом – у. Уравнение линейной статической модели объекта имеет вид:
, а выходом – у. Уравнение линейной статической модели объекта имеет вид:

Необходимо на основе эксперимента вычислить коэффициенты  модели. Экспериментальные точки для входных координат зададим в вершинах гиперпрямоугольника. Точки такого плана для m=2 показаны в верхней части рисунка. Эти точки равномерно распределены относительно известной базовой точки
модели. Экспериментальные точки для входных координат зададим в вершинах гиперпрямоугольника. Точки такого плана для m=2 показаны в верхней части рисунка. Эти точки равномерно распределены относительно известной базовой точки 
Интервалы покачивания  относительно базовой точки задаются экспериментатором, и определяют область изучения объекта. Для этой области строится линейная модель, которая показана на рисунке. С целью унификации процедур построения планов, исследования их свойств, расчета параметров и исследования качества модели осуществляется переход от разменных входных переменных
относительно базовой точки задаются экспериментатором, и определяют область изучения объекта. Для этой области строится линейная модель, которая показана на рисунке. С целью унификации процедур построения планов, исследования их свойств, расчета параметров и исследования качества модели осуществляется переход от разменных входных переменных  к безразмерным
к безразмерным  :
:  .
.
| N | х0 | х1 | х2 | yi |
| + | + | + | y1 | |
| + | - | + | y2 | |
| + | + | - | y3 | |
| + | - | - | y4 |
Точки плана в вершинах прямоугольника (верхняя часть рисунка) в новых координатах оказываются в вершинах квадрата с единичными координатами (нижняя часть рисунка). Центр плана переходит в начало координат. Полный план представлен таблицей:
В этом плане, кроме безразмерных входных переменных х1, х2, введён столбец фиктивной переменной х0 и столбец измерений выхода объекта в каждой точке плана. Фиктивный столбец состоит из +1 и служит для симметрии расчёта всех коэффициентов модели. Для упрощения записи плана единица опускается и указывается только знак единичной координаты.
В новых безразмерных координатах  линейная модель также сохраняет линейный вид:
линейная модель также сохраняет линейный вид:  только с другими параметрами
только с другими параметрами 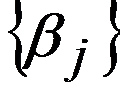 . Подставляем
. Подставляем  ,
,  в уравнение модели и получаем линейное уравнение в координатах
в уравнение модели и получаем линейное уравнение в координатах  .
.

Здесь  .
.
Из этого уравнения получаем алгоритм расчёта коэффициентов  по коэффициентам
по коэффициентам 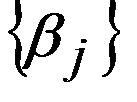 :
: 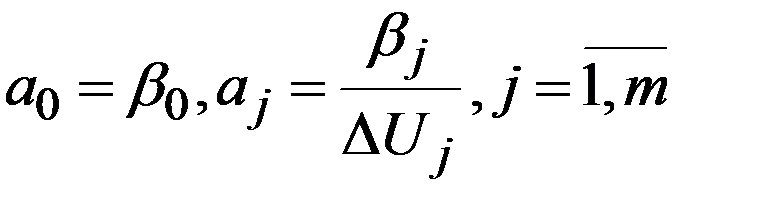 .
.
Коэффициенты  линейной статистической модели оценивают состояние градиента
линейной статистической модели оценивают состояние градиента  от сигнальной части выхода объекта по входным координатам (полиномиальное уравнение объекта), коэффициент
от сигнальной части выхода объекта по входным координатам (полиномиальное уравнение объекта), коэффициент 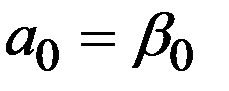 оценивает сигнальную часть
оценивает сигнальную часть  выхода объекта в центре плана
выхода объекта в центре плана  .
.
Заметим, что в новых координатах ( 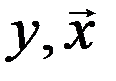 ) полиномиальное уравнение объекта
) полиномиальное уравнение объекта
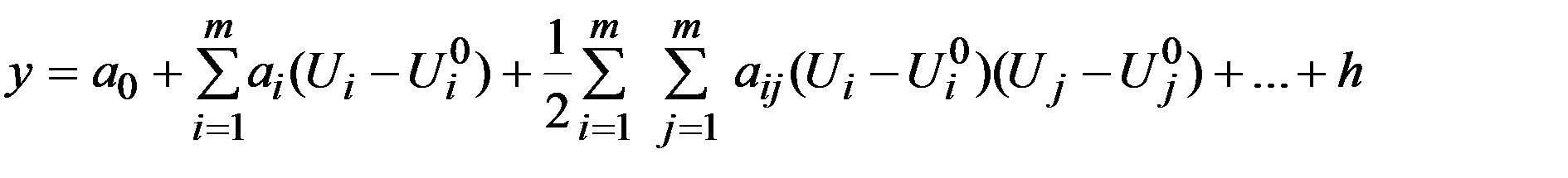
сохраняет свой вид:

Здесь: 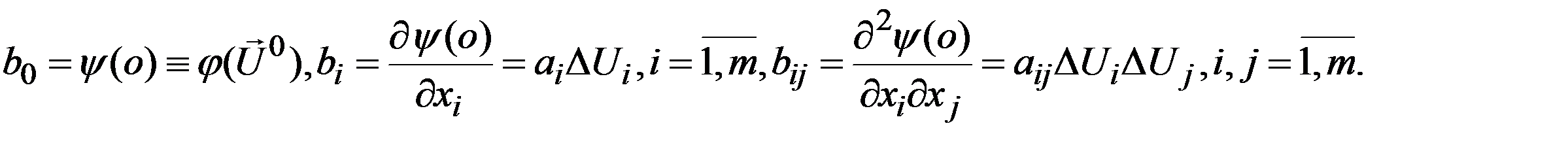
Тогда соответствующая этому уравнению модель объекта в виде отрезка степенного ряда записывается в форме

Здесь N – порядок полинома.
Параметры  модели
модели  рассчитываем по критерию наименьших квадратов
рассчитываем по критерию наименьших квадратов

предполагая, что измерения выхода  некоррелированные и равноточные с дисперсией
некоррелированные и равноточные с дисперсией  Из критерия наименьших квадратов получаем систему линейных алгебраических уравнений:
Из критерия наименьших квадратов получаем систему линейных алгебраических уравнений:

Здесь  - столбцы матрицы планирования, включая фиктивный столбец
- столбцы матрицы планирования, включая фиктивный столбец 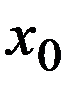 , состоящий из «плюс единиц», у – столбец измерений выхода объекта;
, состоящий из «плюс единиц», у – столбец измерений выхода объекта;  и
и 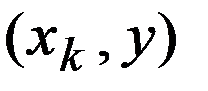 - скалярные произведения столбцов матрицы планирования,
- скалярные произведения столбцов матрицы планирования,
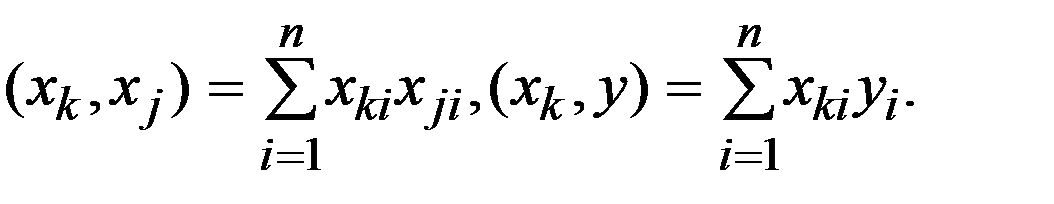
При двух входах объекта (m=2) система линейных алгебраических уравнений имеет вид



Если реализован план, представленный в таблице, то вектор-столбцы х0, х1, х2 взаимно ортогональны в соответствии со скалярным произведением (критерий наименьших квадратов), то есть (х0, х1)=(х0, х2)=(х1, х2)=0. Система уравнений распадается на независимые уравнения, из которых вычисляются параметры модели:

Здесь учтено, что скалярные произведения векторов х0, х1, х2 самого на себя одинаковы и равны количеству измерений. План (таблица), у которого столбцы взаимно ортогональны, называется ортогональным планом. План называется ещё ортогональным планом первого порядка. Последними словами подчёркивается, что он предназначен для построения линейной модели, то есть модели первого порядка.
Дисперсии параметров  одинаковы и равны величине
одинаковы и равны величине 
Параметры  некоррелированны друг с другом, ибо
некоррелированны друг с другом, ибо  В этом не трудно убедиться. Введем обозначения центрированных выходов:
В этом не трудно убедиться. Введем обозначения центрированных выходов:
 , и получим, что
, и получим, что

При использовании ортогонального плана (xj,xi)=0,  . Тогда получаем, что
. Тогда получаем, что 
Дата добавления: 2015-04-18; просмотров: 322; Мы поможем в написании вашей работы!; Нарушение авторских прав |