ОПТИМАЛЬНАЯ ПРОИЗВОДИТЕЛЬНОСТЬ

Модель производительности (1.1) можно использовать для определения числа процессоров N_max, при котором будет достигнута наивысшая производительность ИУС. Это можно сделать, используя тот факт, что в точке максимума тангенс угла наклона касательной к кривой П(N) равен нулю и что он задается производной функции П(N) по N при фиксированных значениях остальных параметров. Переписывая (1.1) в форме

(1.2)

можно легко вычислить требуемую производную:

(1.3)

Если определить N_max как точку, в которой тангенс угла наклона касательной равен нулю

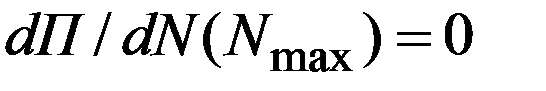, (1.4)

то подставив выражение для 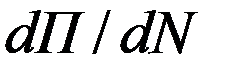из (1.3) в (1.4)

и разрешив полученное уравнение относительно N_max, получим

(1.5)

Обращение производной в 0 является необходимым, но не достаточным условием нахождения абсолютно максимального или минимального значения функции, т.к. функция может содержать несколько максимумов/минимумов, точки перегиба и/или седловые точки, в которых производная так же равна 0.

Все рассуждения верны при существовании производных функции.