
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Архитектура клиент-сервер
 В традиционном понимании система, выполненная в архитектуре "клиент-сервер", представляет собой совокупность взаимодействующих компонент двух типов - клиентов и серверов. Клиенты обращаются к серверам с запросами, серверы их обрабатывают и возвращают результат. Клиент, вообще говоря, может обращаться с запросами к нескольким серверам. Серверы также могут обращаться с запросами друг к другу.
В традиционном понимании система, выполненная в архитектуре "клиент-сервер", представляет собой совокупность взаимодействующих компонент двух типов - клиентов и серверов. Клиенты обращаются к серверам с запросами, серверы их обрабатывают и возвращают результат. Клиент, вообще говоря, может обращаться с запросами к нескольким серверам. Серверы также могут обращаться с запросами друг к другу.
Наиболее часто встречающийся класс приложений, выполненных в архитектуре "клиент-сервер", - различные приложения, работающие с базами данных. В таком случае в качестве сервера выступает СУБД, обеспечивающая выполнение запросов клиента, который, в свою очередь, реализует интерфейс пользователя.
Трехзвенная архитектура ("сервер БД - сервер Приложений - Клиент")
 Развитием архитектуры клиент-сервер является трехзвенная архитектура, в которой интерфейс пользователя, логика приложения и доступ к данным выделены в самостоятельные составляющие системы, которые могут работать на независимых компьютерах.
Развитием архитектуры клиент-сервер является трехзвенная архитектура, в которой интерфейс пользователя, логика приложения и доступ к данным выделены в самостоятельные составляющие системы, которые могут работать на независимых компьютерах.
Разбиение матрицы планирования на блоки (с целью устранения кусочно-постоянного дрейфа).
При проведении эксперимента выход объекта дрейфует. Если этот дрейф кусочно-постоянен, то его можно нейтрализовать, изменяя порядок проведение эксперимента во времени. Для этого разбивают матрицу планирования на блоки и последовательно реализуют (во времени) эту матрицу: вначале один блок, затем другой и т.д.
Рассмотрим ортогональный план  . Считаем, что выход объекта имеет аддитивный дрейф на величину +Δ(когда проводят эксперименты с номерами 1,2,3,4) и на величину –Δ (когда проводят эксперименты 5,6,7,8)
. Считаем, что выход объекта имеет аддитивный дрейф на величину +Δ(когда проводят эксперименты с номерами 1,2,3,4) и на величину –Δ (когда проводят эксперименты 5,6,7,8)
| n | х1 | х2 | х3 | хдр=х1х2х3 | yi | номер блока |
| + | + | + | + | y1=y1ист +Δ | ||
| - | + | + | - | y2=y2ист +Δ | ||
| + | - | + | - | y3=y3ист +Δ | ||
| - | - | + | + | y4=y4ист +Δ | ||
| + | + | - | - | y5=y5ист - Δ | ||
| - | + | - | + | y6=y6ист -Δ | ||
| + | - | - | + | y7=y7ист -Δ | ||
| - | - | - | - | y8=y8ист -Δ |
Этот дрейф приводит к смещению на величину Δ параметра  :
:
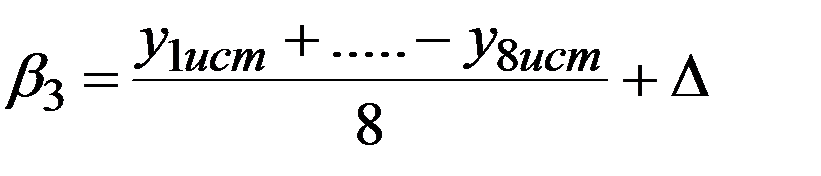 .
.
Для устранения этого недостатка изменим порядок проведения эксперимента, разбив план на два блока. Введем дрейфовую перемену хдр=х1 х2 х3 и по ней получим два блока. Реализуем этот план.
| n | х1 | х2 | х3 | хдр | yi | номер блока |
| + | + | + | + | y1=y1ист +Δ | блок 1 | |
| - | - | + | + | y2=y2ист +Δ | ||
| - | + | - | + | y3=y3ист +Δ | ||
| + | - | - | + | y4=y4ист +Δ | ||
| - | + | + | - | y5=y5ист - Δ | блок 2 | |
| + | - | + | - | y6=y6ист -Δ | ||
| + | + | - | - | y7=y7ист -Δ | ||
| - | - | - | - | y8=y8ист -Δ |
Нетрудно убедиться, что теперь дрейф не смещает параметров линейной модели.
Билет 11
Ортогональное планирование второго порядка (в планировании эксперимента).
Построение планов второго порядка- задача в математическом отношении значительно более сложная, чем в случае построения планов первого порядка. Модель второго порядка при m=3 имеет вид
 .
.
Для вычисления коэффициентов модели второго порядка необходимо варьировать переменные не менее, чем на трех уровнях. Это вызывает необходимость постановки большого числа опытов. Полный факторный эксперимент содержит  точек
точек
| m | |||||||

| |||||||
композиц. план
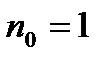
|
Число точек плана равно величине  .
.
Здесь n1- число точек полного факторного эксперимента 2m или дробной реплики 2m-n ; 2m- число парных точек, расположенных на осях координат; 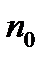 - число опытов в центре плана. Расположение точек в факторном пространстве для композиционного плана Бокса-Уилсона в случае двух и трех входов показано на рисунке.
- число опытов в центре плана. Расположение точек в факторном пространстве для композиционного плана Бокса-Уилсона в случае двух и трех входов показано на рисунке.
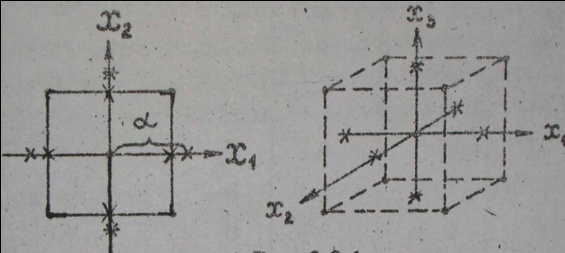
Точки на осях координат называют звёздными точками. Их количество равно удвоенному числу факторов. Расстояние от центра плана до звёздной точки одинаково. Его обозначают буквой α и называют звёздным плечом.
Описанные выше композиционные планы являются центральными планами, ибо все точки плана симметрично расположены относительно центра.
Композиционные планы имеют следующие положительные свойства.
1. Они могут быть получены в результате достройки планов первого порядка, поэтому их иногда называют последовательными планами. Это свойство позволяет при получении неадекватной модели первого порядка перейти к построению модели второго порядка, добавив опыты только в звёздных точках и в центре плана.
2. Дополнительные точки на осях координат и в центре плана (таблица) не нарушают ортогональности для столбцов, соответствующих факторам  и эффектам взаимодействия
и эффектам взаимодействия 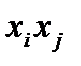 . Этот факт открывает возможность независимого получения соответствующих коэффициентов модели.
. Этот факт открывает возможность независимого получения соответствующих коэффициентов модели.
| n | x0 | x1 | x2 | x1x2 | 
| 
|
| + | + | + | + | + | + | |
| + | - | + | - | + | + | |
| + | + | - | - | + | + | |
| + | - | - | + | + | + | |
| + | 
| 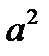
| ||||
| + | - 
| 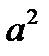
| ||||
| + | 
| 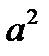
| ||||
| + | - 
| 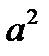
| ||||
| + |
Ортогональность плана нарушается для столбцов 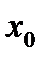 и
и  , ибо
, ибо 
Элементы вышеуказанных столбцов положительны. Чтобы получить полностью ортогональный план, необходимо произвести некоторое преобразование квадратичных переменных и специально выбрать величину α звёздного плеча.
Все элементы каждого столбца 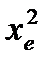 изменим на постоянную величину (среднее арифметическое):
изменим на постоянную величину (среднее арифметическое):

Тогда новые столбцы  ортогональны к
ортогональны к  :
: 
Для выполнения условий ортогональности столбцов  и
и 
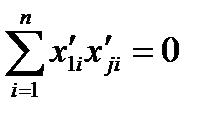
выберем соответствующую величину звёздного плеча α. Эта задача разрешима. В таблице приведены значения α, вычисленные для различного числа независимых переменных
| m | ||||
| Ядро планирования | 22 | 23 | 24 | 25-1 |
Величина 
| 1,000 | 1,215 | 1,414 | 1,547 |
С учётом новых переменных  получаем следующее уравнение модели (для случая m=2):
получаем следующее уравнение модели (для случая m=2):

Параметры  в силу ортогональности плана вычисляются независимо, так же как и при использовании ортогонального плана первого порядка. Пересчитаем коэффициент
в силу ортогональности плана вычисляются независимо, так же как и при использовании ортогонального плана первого порядка. Пересчитаем коэффициент 
который оценивает сигнальную часть выхода объекта в центре плана.
Дата добавления: 2015-04-18; просмотров: 288; Мы поможем в написании вашей работы!; Нарушение авторских прав |