Критерий наименьших квадратов

Считаем, что в каждый момент времени 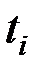(момент измерения входа и выхода объекта) помехи 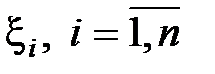, являются центрированными случайными величинами с дисперсиями 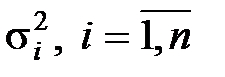. Если дисперсии различны, то измерения называются неравноточными. Считаем также, что , некоррелированны, т. е. 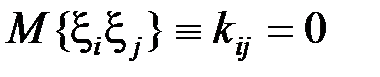при 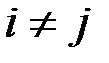. Тогда критерий наименьших квадратов имеет вид

. (6.2.1)

При равноточных измерениях весовые коэффициенты , характеризующие информативность измерений, одинаковы . Тогда имеем

. (6.2.2)

Весовой коэффициент 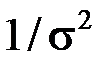теперь на результаты расчетов параметров модели не влияет, поэтому его часто опускают.

Если все помехи 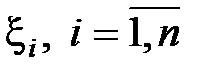, коррелированны, т. е.

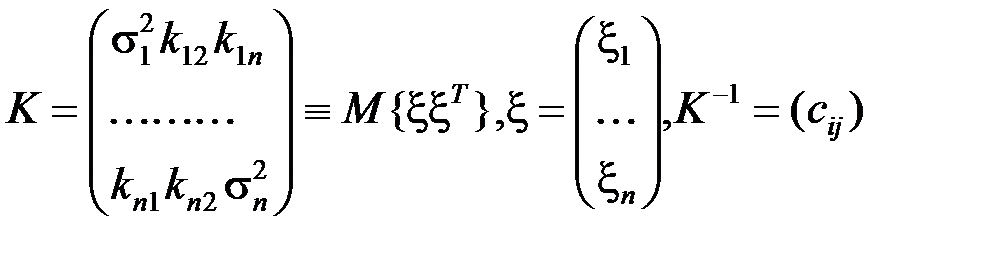, (6.2.3)

то критерий наименьших квадратов базируется на элементах 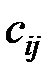матрицы, обратной корреляционной:

. (6.2.4)

Это общая форма критерия. Она включает в себя (при соответствующих упрощениях) все предыдущие формы.

Запишем критерий (6.2.4) в матричном виде. Вводим обозначения:

. (6.2.5)