Билет 14. Кроме рассмотренных видов параметров подпрограмм, версия 7.0 языка позволяет использовать еще один вид параметра - одномерные массивы открытого типаи строки

Кроме рассмотренных видов параметров подпрограмм, версия 7.0 языка позволяет использовать еще один вид параметра - одномерные массивы открытого типаи строки открытого типа. В качестве фактических параметров здесь могут выступать массивы и строки любого размера.

Массив открытого типа - это такой формальный параметр, тип индексов которого, т.е. размер, не объявляется. Он может быть параметром-переменной, параметром-значением и параметром-константой. Индексация элементов массива ведется от нуля, а индекс последней компоненты определяется с помощью функции High. Рассмотрим использование массива открытого типа на примере.

Пример 3. Решить задачу примера 2 с помощью массива открытого типа.

program Otkr_Massiv;

const {Задаем исходные массивы}

a : array[6..10] of real = (1, 2, 3, 4, 5);

b : array[1..4] of real = (6, 7, 8, 9);

function Sum_Otkr(z : array of real) : real; {z - массив открытого типа}

var i : byte; s : real;

begin s := 0;

for i := 0 to High(z) do {Нумерация элементов z от нуля!}

s := s + z[i];

Sum_Otkr := s end; {Sum_Otkr}

begin {Основная программа}

writeln(‘Сумма элементов вектора a = ’, Sum_Otkr(a) : 2 : 0);

writeln(‘Сумма элементов вектора b = ’, Sum_Otkr(b) : 2 : 0);

end.

Итак, массив открытого типа позволяет сократить число передаваемых в подпрограмму параметров.

Итерационные циклы: сумма бесконечного ряда

Запись выражения для 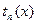на языке Turbo Pascal обычно не вызывает затруднений. Однако есть частные случаи, когда выражение для 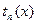содержит целые степени аргумента xи факториалы. В этих случаях применяют следующий прием. Выражают очередное слагаемое как функцию от предыдущего слагаемого: или

, (2)

где . (3)

Ниже приведен алгоритм нахождения суммы бесконечного ряда с использованием вспомогательной функции для конкретного примера.

Пример 1. Вычислить с погрешностью e=0,001 для заданного значения аргумента x значение функции sin(x) с помощью ее разложения в ряд:

,

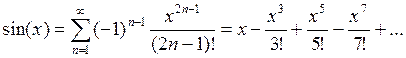где (2n – 1)! = 1×2×3××× (2n – 1).

Выразим вспомогательную функцию из выражения (3):

.

С ее помощью по формуле (2) будем определять очередное слагаемое t. Первый член ряда находим непосредственно из формулы для общего члена ряда, подставив в нее n = 1. Далее приведен алгоритм решения задачи.

Запишем алгоритм на языке программирования:

program Summa_Ryada;

const

e = 0.001;

var

n: byte;

fi, summa, t, x: real;

begin

writeln(‘Введите x’);

readln(x);

summa:=0; t:=x; n:=2;

while abs(t) > e do begin

summa:=summa + t;

fi:=- x*x/(2*n-2)/(2*n-1);

t:=t*fi;

n:=n + 1

end; {while}

writeln(‘Сумма ряда = ‘, summa);

writeln(‘Учтено ‘, n-1, ‘ слагаемых’);

writeln(‘Синус = ‘, sin(x))

end.