Билет 18

1. Маржинальный анализ, показатели и методика его проведения.

Ответ: В основе маржинального анализа лежит поведение затрат, т.е. маржинальный анализ предназначен для анализа затрат, расчета прибыли, установления цен на производимую продукцию. Затраты бывают: 1) переменные, т.е. которые изменяются пропорционально уровню деловой активности; 2) постоянные, т.е. которые не меняются (амортизация, оплата коммунальных услуг). Маржинальный анализ – соотношение между затратами, объемами продаж и прибылью. Дальше схема из телефона. Т – точка безубыточности объема реализованной продукции, Дм – маржинальный доход, Ду – удельный вес маржинального дохода в выручке от реализованной продукции, Дс - ставка маржинального дохода в цене за единицу продукции, П - прибыль, Н – постоянные затраты, Рn – переменные затраты, ВР - выручка от реализованной продукции, К - кол-во продан продукции в натуральную единицу,V - удельные переменные затраты, Р – цена единицы продукции Дм=П+Н=ВР-Рn, формула для расчета точки Т в денежном измерении:

Т/Н=В/Дм => Т=ВР*Н / Дм, или Т=Н / (Дм / ВР)=Р/Ду.

В натуральных единицах: Т=К*Н / Дм

Дс=Дм / К=>Дм=К*Дс

Т=К*Н / Дм=К*Н / Дс*К=Н/Дс,

Дс=Р-V => Т=Н / Дс=Н / (Р-V)

Зона безопасности: ЗБ=(ВР-Т) / ВР * 100%.

Безубыточность V продаж и зона безопасности зависят от суммы постоянных и переменных затрат, а также от уровня цен на продукцию. Оптимальным считается тот план, который позволит снизить долю постоянных затрат на единицу продукции, уменьшить безубыточность V продаж и увеличить зону безопасности.

2. Способ пропорционального деления и долевого участия при оценке влияния факторов в детерминированном анализе.

Ответ: Сущность способа пропорционального деления состоит в пропорциональном делении прироста результативного показателя по факторам его обусловившим, а долевого участия — в определении доли участия каждого фактора в общем приросте результативного показателя.

Эти способы применяются для аддитивных, мультипликативных, кратных и смешанных моделей типа .

Для определения влияния отдельных факторов на прирост результативного показателя рассчитывается один из следующих коэффициентов:

1) коэффициент пропорционального деления , как отношение общего относительного прироста результативного показателя к сумме относительных изменений факторных показателей.

При аддитивных типах моделей рассчитывается один коэффициент пропорциональности, а при других типах моделей — он определяется для каждого порядка факторов в отдельности.

При исходной модели ,

(изменения всех составляющих взяты в относительных единицах).

;

; ;

.

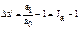2) коэффициент долевого участия , который определяется как отношение относительного прироста i‑го факторного показателя к сумме относительных изменений факторных показателей.

Например, для исходной факторной модели , коэффициент долевого участия для фактора «а»:

.

Тогда для приведенной исходной мультипликативной модели:

;

;

;

.

Переход от относительных единиц к абсолютным осуществляется по формулам:

; .

Если взаимосвязь факторов двух уровневая (n-уровневая), то необходимо рассчитывать коэффициент пропорционального деления для каждого уровня, а коэффициент долевого участия для каждого факторного показателя соответствующего уровня.

Задача

Используя исходную кратную модель коэффициента оборачиваемости активов, определить: объем годовой выручки от продаж, если среднегодовая сумма активов – 500 тыс. руб., рентабельность активов – 40%, рентабельность продаж – 25%.

Ответ:

0,40=х/500

Х=200

Пр=200

Х=200/0,25= 800