Управляемость и наблюдаемость динамических систем

Для линейных динамических систем, представленных на рис. 1, и описываемых уравнениями в пространстве состояний порядка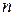

,

,

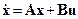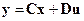полная управляемость означает существование ограниченного входного сигнала 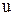, переводящего объект за конечный интервал времени из любого начального состояния 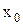в любое наперёд заданное состояние . Если бы объект не был полностью управляемым, то нельзя рассчитывать на то, что замкнутой системе, содержащей этот объект, можно придать любые динамические свойства, т.е. желаемое расположение корней.

Условием полной управляемости объекта является равенство ранга его матрицы управляемости 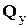порядку 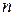объекта. Матрица управляемости выражается через параметры объекта формулой

.

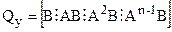Матрица записана в блочной форме. Если элементы – блоки записать в развернутой форме, то матрица станет прямоугольной типа .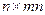

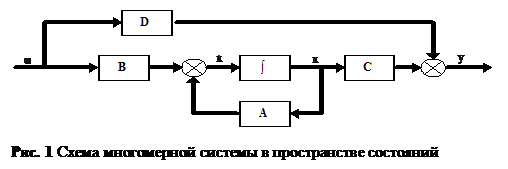
Наблюдаемость – произвольное состояние можно найти по имеющимися записям вектора выходного сигнала (t>t₀ ). Условием наблюдаемости является равенство ранга матрицы Q порядку системы n :