Свойство сохранения зависимости

Определение проекции множества функциональных зависимостей F на схему отношения R_i.

Пусть – схема БД, F – исходное множество функциональных зависимостей.

Проекцией F на R_i называется множество функциональных зависимостей таких, что имеет место следующее включение: .

Проекция F на R_i обозначается: .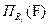

Определение свойства сохранения зависимости

Схема БД ρ обладает свойством сохранения зависимости, если справедливо следующее равенство:

.

Данное выражение читается следующим образом:

1) Берется .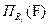

2) Полученные функциональные зависимости объединяются.

3) Для этих зависимостей строится замыкание (применяются аксиомы Армстронга).

4) Полученное множество функциональных зависимостей сравнивается с F⁺.

Пример схемы БД, не обладающей свойством сохранения зависимости.

Пусть – универсальная схема отношения, – схема БД, а – функциональная зависимость.

Доказать, что ρ не обладает свойством сохранения зависимости.

;

.

Найдем такую функциональную зависимость, которая принадлежит F⁺, но не принадлежит левой части выражения в определении свойства сохранения зависимости. И тем самым докажем, что ρ не обладает свойством соединения без потерь.

В качестве такой зависимости имеем:

(по определению). (**)

. (*)

Для доказательства последнего утверждения требуется построить на объединенном множестве функциональных зависимостей и проверить ?

, но .

Это доказывает утверждение (*).

(*) и (**) доказывают утверждение задачи (что ρ не обладает свойством сохранения зависимости), т.е. .

Пример схемы БД, обладающей свойством сохранения зависимости.

Пусть – универсальная схема отношения, – схема БД, а – функциональная зависимость.

Доказать, что ρ обладает свойством сохранения зависимости.

– все зависимости, полученные из F с помощью аксиом Армстронга.

Т.о. равенство доказано и данная схема БД обладает свойством сохранения зависимости.

2. Планирование тиражирования данных со вторичного сервера.